Độ lồi của trái phiếu

1. Độ lồi của trái phiếu không có quyền chọn

Thời gian hoàn trả trung bình điêu chỉnh cho phép ước lượng sự thay đổi giá của trái phiếu theo sự thay đổi lãi suất thị trương. Tuy nhiên, việc ước lượng giá của trái phiéu bằng cách này chi chính xác với sự thay đổi rất nhỏ của lãi suất thị trường. Nếu lãi suất thị trường biến động lớn, thời gian hoàn trả trung bình điều chinh sê có dạng cong. Để hiểu được tác động của độ lồi trái phiếu, cần phải xét mối quan hệ giá – lãi suất với từng trái phiếu.

Đường cong giá – lãi suất cung cấp một tập hợp giá cả của một trái phiếu tại một thời điểm cụ thể.

 

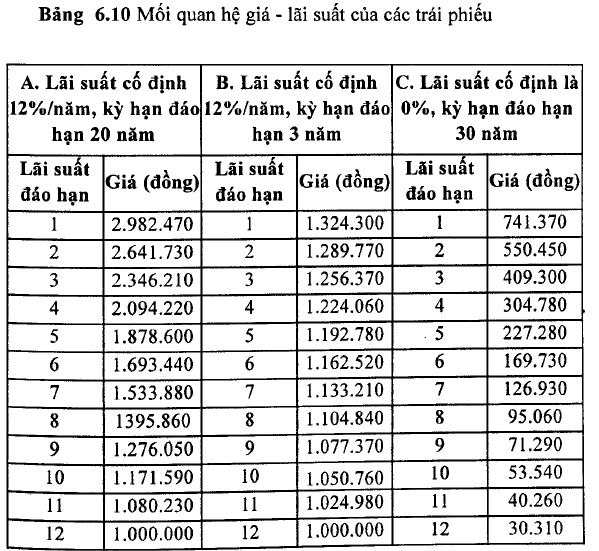
Đường biểu diễn quan hệ lãi suất thị trường (lãi suất đáo hạn) – giá của trải phiếu trong các trường hợp này không phải là đường thẳng mà là đường cong.

Hình 6.7 Quan hệ lãi suất – giá của trái phiếu

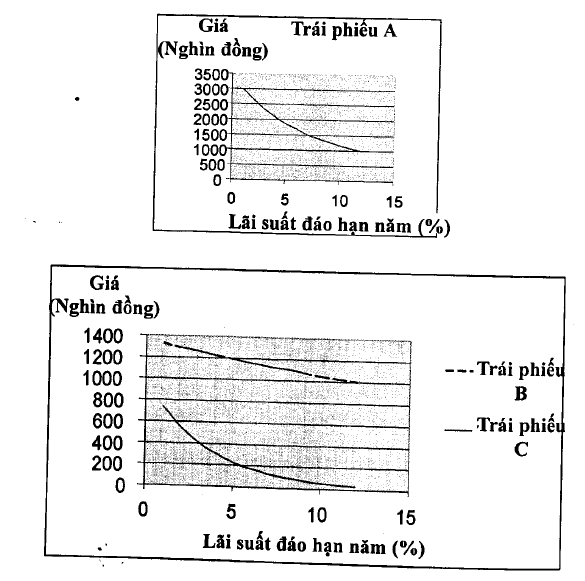
Hai điểm quan trọng về mối quan hệ lãi suất – giá cần lưu ý:

Thứ nhất, quan hệ này cỏ thể mô tả cho 1 trái phiếu đơn hay 1 đanh mục đầu tư trái phiếu.

Thứ hai, đường cong biểu diễn mối quan hệ giá – lãi suất của các trái phiếu khác nhau sẽ cỏ những điểm khác nhau, phụ thuộc vào đặc điểm của dòng tiền (lãi suất cố định, kỳ hạn).

Ví dụ 6.20: Đường biểu diễn mối quan hệ giá – lãi suất đối với trái phiếu ngắn hạn có lãi suất cao hầu như sẽ là 1 đường thẳng, vì giá không thay đổi nhiều bằng sự thay đổi lãi suất (ví dụ trái phiếu kỳ hạn 3 năm, lãi suất 12%/năm trong bảng 6.10). Ngược lại, đường biểu diễn mối quan hệ cho trái phiếu dài hạn lãi suất thấp sẽ là 1 đường cong, như trường hợp trái phiếu 30 năm lãi suất cố định bằng 0 trong bảng 6.10. Sự khác nhau về độ cong này đã được biểu hiện rõ trong bàng 6.10. Độ cong của đường quan hệ lãi suất – giả được xem như là độ lồi của trái phiếu.

Theo hình 6.7, do độ cong của đường quan hệ giá – lãi suất, khi lãi suất tăng, giá trái phiếu giảm và giảm chậm dần. Tương tự, khi lãi suất giảm, giá trái phiếu tăng với tốc độ cao dần. Vì vậy, độ lồi được xem là một đặc điểm đáng xem xét. Cụ thể, nếu nhà đầu tư có 2 trái phiếu với thời gian đáo hạn trung bình bằng nhau, nhưng 1 trái phiếu có độ lồi lớn hơn, nhà đầu tư sẽ muốn sở hữu trái phiếu đó hơn vì đem lại hiệu suất giá tốt hơn khi lãi suất tăng (giá trái phiếu giảm ít hơn) hay lãi suất giảm (giá trái phiếu tăng nhiều hơn).

Cho trước đường giá – lãi suất, thời gian hoàn trả trung bình điều chỉnh là % thay đổi giá so với sự thay đổi của lãi suất như sau:

MD = (dP/dr)/P                       (6.21)

Đường dP/dr là tiếp tuyến của đường cong giá – lãi suất tại 1 mức lãi suất cho sẵn như được biểu diễn ở hình 6.8. Với thay đổi nhỏ của lãi suất (ví dụ từ y* tới cả yj hay y-ì ), đường thẳng này sẽ dự đoán giá mới của trái phiếu ít hơn giá trị thực được xác định từ đường cong giá – lãi suất. Sự sai lệch trong dự đoán này là do thời gian hoàn trả trung bình điều chinh là một đường cong ước lượng. Cụ thể, ước lượng giá sử dụng thời gian hoàn trả trung bình điều chỉnh sẽ thấp hơn giá trị thực tăng lên do lãi suất giảm, và ước lượng vượt quá độ giảm giá thực gây ra do lãi suất tăng. Đồ thị này chứng minh tác động của độ lồi và cũng chỉ ra rằng sự thay đổi giá không đối xứng khi lãi suất thị trường tăng hay giảm. Khi giá giảm thì cổ sự sai lệch lớn hom là khi giá tăng, do căn cứ vào độ lồi, khi lãi suất giảm, giá tăng với tỷ lệ tăng dần, trong khi giá giảm với tỳ lệ giảm dần khi lãi suất tăng.

Hình 6.8 Sử dụng thời gian hoàn trả trung bình điều chỉnh để ước lượng giá cổ phiếu

Sai lệch trong ước lượng giá trái phiếu chỉ dựa vào thời gian hoàn trả trung bình điều chỉnh Sai lệch trong ước lượng giá trái phiếu dựa vào thời gian

Độ lồi là một đom vị đo lường của đường cong quan hệ giá – lãi suất. Bởi vì thời gian hoàn ừả trung bình điều chỉnh là độ dốc của đường cong tại 1 mức lãi suất, độ lồi xác định sự thay đổi trong thời gian hoàn trả trung binh, về mặt toán học, độ lồi là đạo hàm của giá so với lãi suất (d²P/dr²) chia cho giá. Cụ thể, độ lồi là % thay đổi dP/dr cho 1 sự thay đổi lãi suất:

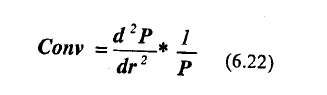
Độ lồi là một đom vị đo lường xem đường giá – lãi suất của 1 trái phiếu lệch khỏi đường xấp xi với nó là bao nhiêu. Theo hình 6.7 và 6.8, đối với trái phiếu không được hoàn trả trước hạn, độ lồi luôn là một sổ dưomg (+), điều này hàm ý rằng đường giá – lãi suất nằm trên đường thời gian hoàn trả trung bình điều chỉnh. Hình 6.7 chứng minh quan hệ về giá – lãi suất của 2 trái phiếu với kỳ hạn và lãi suất khác nhau.

Mối quan hệ giữa 3 nhân tố (lãi suất ưái phiếu, kỳ hạn, lãi suất thị trường) và độ lồi của trái phiếu như sau:

• Mối quan hệ ngược chiều giữa lãi suất trái phiếu và độ lồi của ừái phiếu (với lãi suất thị trường và kỳ hạn không đổi): Lãi suất trái phiếu càng thấp, độ lồi trái phiếu càng lớn.
• Mối quan hệ thuận chiều giữa kỳ hạn trái phiếu và độ lồi của trái phiếu: Kỳ hạn đáo hạn của trái phiếu càng dài, độ lồi của trái phiếu càng lớn.
• Mối quan hệ ngược chiều giữa lãi suất thị trường và độ lồi của rái phiếu. Điều này có nghĩa đường giá – lãi suất cong hơn với mức lãi suất thấp hơn.

2. Tác động của độ lồi – thời gian hoàn trả trung bình điều chỉnh của trái phiếu lên giá trái phiếu

Giá trái phiếu biến động do sự thay đổi lãi suất thị trưởng chịu tác động của hai nhân tố: Thời gian hoàn trà trung bình điều chinh và độ lồi của trái phiếu. Tác động của 2 nhân tố này lên giá trái phiếu tùy thuộc vào đặc điểm của từng trái phiếu như sau:

Trái phiếu có độ lồi lớn và lãi suất thay đổi lớn thì tác động của độ lồi đến giá trái phiếu sẽ lớn. Ngược lại, lãi suất thay đổi nhỏ thỉ tác động của độ lồi đến giá trái phiếu nhỏ.

Trái phiếu cỏ tác động của độ lồi nhỏ, lãi suất thay đổi nhỏ thi tác động của độ lồi nhỏ.

Từ thời gian hoàn trả trung bình điều chinh, có thể biết được % thay đổi giá trái phiếu dựa vào % thay đổi lãi suất và sự ước lượng chi chính xác lãi suất thay đổi nhỏ. Tuy nhiên, cần phải xem xét tác động của độ lồi lên sự thay đổi giá trái phiếu khi có sự thay đổi lớn về lãi suất và/hoặc khi trái phiếu có độ lồi lớn.

Với PV(CF) là giá trị hiện tại của dòng tiền từ trái phiếu.

Ví dụ 6.21: Một trái phiếu cỗ kỳ hạn 3 năm, lãi suất 12%/năm và lãi suất đảo hạn của trái phiếu là 9%/năm, mệnh giá ứái phiếu 100 nghìn đồng, tiền lãi trái phiếu được trả hằng năm. Hãy tính độ lồi của trái phiếu?

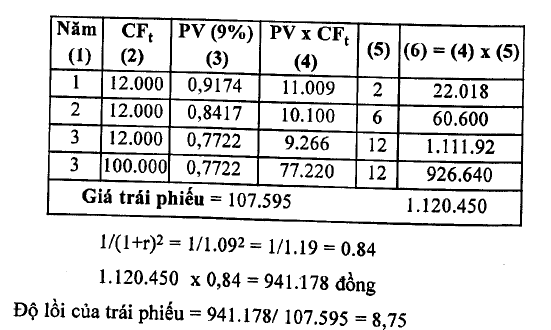
Do đó, thay đổi giá trái phiếu khi lãi suất thay đổi như sau:

• Thay đổi giá trái phiếu do thời gian hoàn trả trung bình của trái phiếu:
• MD X Giá trái phiếu X Ar
• Thay đổi giá trái phiếu do độ lồi của trái phiếu

V2 X Giá trái phiếu X Độ lồi X (A thay đổi lãi suất)²

• Thay đổi giá trái phiếu do thời gian hoàn trả trung bình và do độ lồi của trái phiếu:

AP = AP do thời gian hoàn trả trung bình + AP do độ lồi

Ví dụ 6.22: Trái phiếu B có thời hạn đáo hạn 18 năm, lãi suất cố định 12%/năm, lãi suất đáo hạn 9%/năm. Giá cùa trái phiếu 126.500 đồng, thời gian hoàn trả trung bỉnh điều chinh 8,38, độ lồi của trái phiếu là 107,7. Hãy tính sự thay đổi giá của trái phiếu dựa vào thời gian hoàn trả trung bình điều chinh và độ lồi của trái phiếu?

ước lượng sự thay đổi giá trái phiếu sử dụng thời gian hoàn trả trung bình điều chinh:

Trường họp B: Thay đổi cùa lãi suất: -300 cơ bản

Thay đổi giá trái phiếu do thời gian hoàn trả trung bình là:

– 8,38 X (-300/100) = + 25,14% 126.500 X 25,14% = 31.802 đòng

Thay đổi giá trái phiếu do tác động của độ lồi:

^lA X (126.500) X 107,70 X (0,03)2 6.812.030 X 0,0009 = 6.110 đồng

Tác động kép về thay đổi giá trái phiếu = Thay đổi giá trái phiếu do thời gian hoàn trả trung bình + Thay đổi giá trái phiếu do tác động của độ lồi = 31.802 + 6.110 đồng

Giá dự kiến củaừái phiếu là: 126.500 + 31.802 + 6.110=164.412 đồng.