Đầu tư tài chính
Phân bổ vốn giữa tài sản rủi ro và tài sản phi rủi ro
Những nhà quản trị danh mục đầu tư luôn tìm cách đạt đến sự cân bằng tốt nhất có thể có giữa rủi ro và lợi tức. Để đạt được thành quả này, nhiệm vụ đầu tiên là đưa ra quyết định phân bổ vốn.
Sự chọn lựa đầu tư vào tài sản rủi ro là bước khởi đầu trong quyết định phân bổ vốn của nhà đầu tư. Trong bước này, nhà đầu tư sẽ phải quyết định loại chứng khoán để nắm giữ. Thực tế, hầu hết những nhà đầu tư tổ chức đều lựa chọn chứng khoán rủi ro (chẳng hạn như cổ phiếu thường) theo cách tiếp cận top – down. Theo cách tiếp cận này, việc lựa chọn chứng khoán tốt để đầu tư phải diễn ra theo quy trình, bắt đầu từ phân tích môi trường vĩ mô, kế đến là môi trường ngành và sau cùng là phân tích công ty. Sau khi lựa chọn chứng khoán rủi ro tốt để đầu tư, nhà đầu tư tiếp tục quyết định bao nhiêu phần trăm vốn được phân bổ vào những tài sản này và bao nhiêu phằn trăm vốn được đầu tư vào các tài sản an toàn hơn ở trên thị trường tiền tệ. Phần này sẽ đề cập một trong những quyết định phân bổ vốn phổ biến nhất trong lý thuyết quản trị danh mục đầu tư – quyết định phân bổ vốn giữa một tài sản phi rủi ro với một tài sản rủi ro (hoặc một danh mục tài sản rủi ro).
Trong quy trình phân bổ vốn này. đầu tiên chúng ta xác định sự đánh đổi giữa rủi ro và lợi tức khi chọn lựa giữa tài sản rủi ro và tài sản phi rủi ro. Sau đó, chúng ta sẽ chỉ ra mức độ ngại rủi ro của nhà đầu tư tác động như thế nào đến phương án kết hợp tối ưu giữa hai loại tài sản nói trên.
1 Phân bổ vốn giữa tài sản (hoặc danh mục tài sản) rủi ro và tài sản phỉ rủi ro
Thông thường, trái phiếu công ty dài hạn và cổ phiếu thường là những tài sản tài chính có rủi ro cao hơn tín phiếu kho bạc. Tuy vậy. những tài sản có rủi ro cao hơn thường mang lại mức lợi tức kỳ vọng cao hơn. Nhà đầu tư có thể đầu tư một phần vốn vào tài sản rủi ro và phần còn lại vào tài sản phi rủi ro. Chẳng hạn, đầu tư một phần vốn vào tín phiếu kho bạc, và phần còn lại vào các tài sản có rủi ro cao hơn như các loại cổ phiếu thường.
Chúng ta ký hiệu danh mục đầu tư gồm các tài sản rủi ro là p và tài sản phi rủi ro là F. Khi có sự phân bổ lại giữa tỷ trọng đầu tư vào danh mục đầu tư rủi ro p và tài sản phi rủi ro F, chúng ta giả định không thay đổi tỷ trọng của những tài sản rủi ro trong danh mục rủi ro p ban đầu. Danh mục P và F sẽ được kết hợp trong danh mục đầu tư tổng thể hay còn gọi là danh mục kết hợp, ký hiệu là danh mục c.
Xem xét tình huống dưới đây, giả định rằng tổng giá trị vốn đầu tư ban đầu của một nhà đầu tư là 100 triệu đồng. Trong đó, 25 triệu đồng được đầu tư vào tín phiếu kho bạc F (tài sản phi rủi ro). Phần vốn còn lại là 75 triệu được đầu tư vào danh mục chứng khoán rủi ro, trong đó
45 triệu được đầu tư vào cổ phiếu thường (E) và 30 triệu vốn đầu tư còn lại là vào trái phiếu công ty dài hạn (B). cổ phiếu thường và trái phiếu công ty dài hạn tạo nên danh mục đầu tư rủi ro, p, với tỷ trọng của:

Danh mục rủi ro p chiếm 75% trong danh mục đầu tư kết hợp c.
Giả sử trên cơ sở dự báo khá bi quan về triển vọng của thị trường chứng khoán, chủ sở hữu danh mục đầu tư kết hợp này mong muốn giảm rủi ro bằng cách giảm tỷ trọng phân bổ vốn vào danh mục rủi ro từ 75% xuống còn 60%. Giá trị danh mục rủi ro khi đó còn lại là: 60% X 100 triệu đồng = 60 triệu đồng, số tiền giảm là 15 triệu đồng sẽ được sử dụng để đầu tư thêm vào tín phiếu kho bạc (tài sản phi rủi ro), số tiền đầu tư vào tài sản phi rủi ro sẽ tăng lên là 100 triệu đồng X (100% – 60%) = 40 triệu đồng, nghĩa là tăng thêm 15 triệu đồng.
Tuy nhiên điểm mấu chốt ở đây là chúng ta đã giả định tỷ trọng của mỗi tài sản trong danh mục rủi ro không thay đổi. Bởi vì, tỷ trọng của E và B trong danh mục đầu tư rủi ro lần lược là 60% và 40%, chủng ta bán
60% X 15 triệu đồng = 9 triệu đồng cùa E và 40% X 15 triệu đồng = 6 triệu đồng của B. Sau khi bán, tỷ lệ của mỗi loại tài sản trong danh mục rủi ro vẫn không thay đổi:
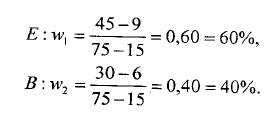
2. Danh mục đầu tư bao gồm một tài sản rủi ro và một tài sản phi rủi ro
Để đơn giản hóa, chúng ta xem xét hành vi của nhà đầu tư khi có sự thay đổi trong tỷ suất lợi tức kỳ vọng và rủi ro của danh mục đầu tư kết hợp bằng cách thay đổi hỗn hợp giữa tài sản rủi ro và tài sản phi rủi ro. Miễn là chúng ta không thay đổi tỷ trọng của mỗi loại chứng khoán trong danh mục rủi ro, phân phối xác suất của tỷ suất lợi tức trên danh mục rủi ro được giữ nguyên khi phân bổ lại tài sản.
Giả định rằng nhà đầu tư quyết định đầu tư vào một danh mục đầu tư kết hợp c bao gồm danh mục tài sản rủi ro p với tỷ trọng là y% và tài sản phi rủi ro F với tỷ trọng là (l-y)%.
Gọi tỷ suất lợi tức và tỷ suất lợi tức kỳ vọng trên danh mục p lần lượt là Rp và E(Rp) và độ lệch chuẩn của tỷ suất lợi tức là Qp. Tỷ suất lợi tức của tài sản phi rủi ro là Rß
Xem xét ví dụ sau: E(Rp) = 15%, Op = 22%, và tỷ suất lợi tức trên tài sản phi rủi ro F là E(Ry) = 7% (chú ý là Oß ~ 0). Vậy phần bù rủi ro của danh mục p là E(Rp) – Rß = 8%.
Với tỷ trọng y% trên danh mục đầu tư rủi ro và (l-y)% trên tài sản phi rủi ro, tỷ suất lợi tức kỳ vọng trên danh mục đầu tư kết hợp, c, sẽ là:
E{RC) = yE(Rp) + (1 – y)Rf (2,1)
Thay số, ta có: tỷ suất lợi tức kỳ vọng của DMĐT kết hợp c là:
E(RC) = 1 + y{\S-l)
Kết quả này cho thấy rằng tỷ suất lợi tức cơ bản nhất của bất kỳ một danh mục đâu tư nào là tỷ suât lợi tức phi rủi ro. Ngoài ra, phần bù rủi ro của danh mục đầu tư kết hợp gẽ phụ thuộc vào phần bù rủi ro của danh mục đầu tư rủi ro, E(Rp) – Rỵ và tỷ trọng của danh mục rủi ro, y%. Ờ đây, chúng ta giả định các nhà đầu tư là những người ngại rủi ro và do vậy họ chỉ đầu tư khi có một phần bù rủi ro đi kèm với danh mục đầu tư rủi ro.
Độ lệch chuẩn của tài sản phi rủi ro bằng 0. Khi chúng ta kết hợp một tài sản rủi ro với một tài sản phi rủi ro trong một danh mục đầu tư. độ lệch chuẩn của danh mục đầu tư kết hợp là độ lệch chuẩn của tài sản rủi ro nhân với tỷ trọng của tài sản rủi ro trong danh mục kết hợp đó:

Công thức (2.2) cho thấy độ lệch chuẩn của DMĐT kết hợp tỷ lệ với cả độ lệch chuẩn của tài sản rủi ro cũng như tỷ trọng đầu tư vào nó.
Hình 2.1 dưới đây biểu diễn tập hợp những cơ hội đầu tư có thể có giữa một tài sản rủi ro và một tài sản phi rủi ro xét trong mối tương quan giữa lợi tức và rủi ro. Tài sản phi rủi ro F nằm trên trục tung bởi vì độ lệch chuẩn của nó bằng 0. Tài sản rủi ro p được biểu diễn tương ứng với độ lệch chuẩn là 22% và lợi tức kỳ vọng là 15%. Nếu một nhà đầu tư lựa chọn đầu tư hoàn toàn vào tài sàn rủi ro, thi y = 100% (hay 1 – y = 0%) và khi đó danh mục đàu tư kết hợp c sẽ trùng với danh mục p. Nếu lựa chọn ngược lại thì y = 0% (hay 1 – y = 100%) và danh mục đầu tư kết hợp c sẽ trùng với danh mục đầu tư phi rủi ro F.
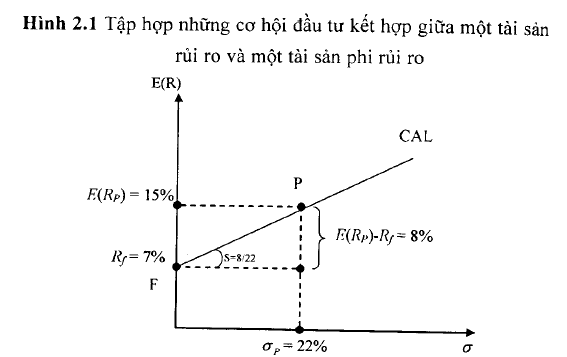
Vậy, các danh mục có tỷ trọng y nằm trong khoảng 0 và 1 có đặc điểm gì? Những danh mục này sẽ nằm trên đường thẳng nối điểm F và p. Độ dốc của đường thẳng này bằng [E(Rp) – Rf]/ơp trong ví dụ này là 8/22. Điều này có thể được giải thích như sau: phần lợi tức tăng thêm trên mỗi đơn vị rủi ro tăng thêm là 8/22 = 0,36.
Để rút ra một phương trình chính xác biểu diễn mối quan hệ trên đường thẳng nối giữa F và p, chúng ta sắp xếp lại phương trình 2.2 bằng cách thay y = ơc / Op vào phương trình 2.1 để mô tả sự đánh đổi giữa tỷ suất lợi tức kỳ vọng và độ lệch chuẩn:
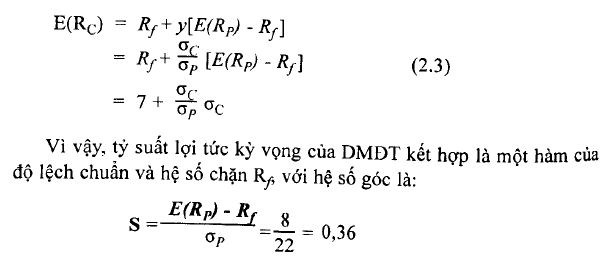
Hình 2.1 đã chi rõ một tập hợp những cơ hội đầu tư thông qua việc
kết hợp sự đánh đổi giữa tỷ suất lợi tức kỳ vọng và độ lệch chuẩn đối với tất cả các danh mục đầu tư trên cơ sở thay đổi giá trị tỷ trọng y. Tập hợp những điểm này hình thành nên đường thẳng bắt đầu từ Ry-và đi qua điểm R Đường thẳng này được gọi là đường phân bổ vốn (CAL, Capital Allocation Line). Đường phân bổ vốn thể hiện tất cả các kết hợp có thể có giữa một tài sản rủi ro (hoặc danh mục đầu tư rủi ro) và một tài sản phi rủi ro. Hệ số góc của đường CAL, ký hiệu s, tương xứng với sự tăng lên của tỷ suất lợi tức kỳ vọng trong danh mục đầu tư kết hợp trên mỗi đơn vị tăng thêm của rủi ro (độ lệch chuẩn). Vì lý do này, hệ số góc của đường CAL còn được gọi là tỷ lệ phần thưởng trẽn rủi ro.
Trong trường hợp danh mục đầu tư được chia đều giữa tài sản rủi ro và tài sản phi rủi ro (y=0,5), tỷ suất lợi tức kỳ vọng E(RCJ = 7 + 0,5 X 8 = 11 %, phần bù rủi ro là 4% và độ lệch chuẩn Gc = 0,5×22 =11%. Nó sẽ nằm ở giữa điểm F và p trên đường thẳng FP. Tỷ lệ phần thưởng trên rủi ro s = 4/11 = 0,36 và cũng hoàn toàn bằng với tỷ lệ của danh mục đầu tư rủi ro p, 8/22 = 0,36.
Mở rộng hơn, những điểm nằm về phía phải của danh mục đầu tư p trên đường CAL có đặc điểm gì? Neu nhà đầu tư có thể đi vay tại mức lãi suất phi rủi ro là = 7%, họ có thể xây dựng được những dự án đầu tư nằm về phía phải của điểm p trên đường CAL.
Giả sử ngân sách đầu tư là 100 triệu đồng, và nhà đầu tư vay thêm một khoản là 20 triệu đồng. Tất cả ngân sách này được đầu tư vào tài sản rủi ro. Đây là đòn bẩy tài chính trong tài sản rủi ro. Trong trường hơp này:

Như vậy, danh mục đầu tư có sử dụng đòn bẩy tài chính có độ lệch chuẩn cao hơn so với danh mục đầu tư không sử dụng đòn bẩy tài chính vào tài sản rủi ro.
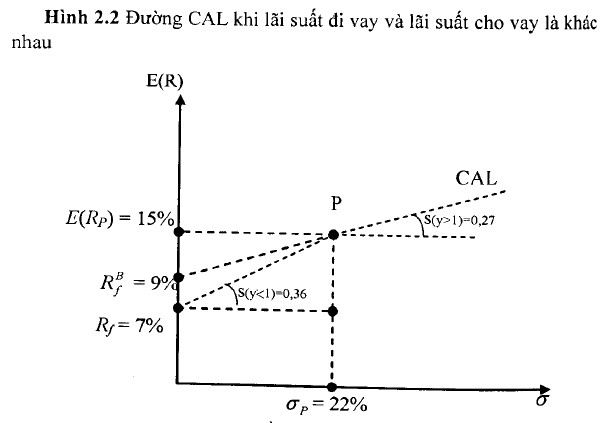
Chú ý quan trọng là những nhà đầu tư cá nhân không có khả năng đi vay tại mức lãi suất phi rủi ro. Rủi ro vỡ nợ khiến người cho vay yêu cầu lãi suất cho vay cao hơn, Vì vậy, chi phí đi vay của những nhà đầu tư phi chính phủ sẽ cao hơn mức lãi suất phi rủi ro Ry= 7%. Giả sử lãi suất đi vay là R B – 9%. Khi đó, tỷ lệ phần thưởng trên rủi ro (hệ số góc của đường CA¿) sẽ là [E(Rp) – Rb] ỉö = 6/22 = 0,27. Do đó, đường CAL sẽ bị “gấp khúc” tại điểm p (x/m Hình 2.2). về phía trái của điểm p, nhà đầu tư đang cho vay với mức lãi suất 7%, và hệ số góc của đường CAL trường hợp này là 0,36. về phía phải của điểm p có y>l, nhà đầu tư sẽ đi vay tại mức lãỉ suất 9% để tài trợ cho việc đầu tư thêm vào tài sản rủi ro và hệ số góc lúc này là 0,27.
không được vượt quá 50% giá trị thanh toán. Vì thế, nếu giá trị thực tế của tài khoản của nhà đầu tư là 100 triệu đồng, nhà môi giới chỉ cho vay tối đa 100 triệu đồng để mua thêm cổ phiếu. Khi đó, người này sỗ có 200 triệu đồng ở bên tài sản có và 100 triệu đồng bên tài sản nợ, với y = 2,0.
3. Chấp nhận rủi ro và sự phân bổ tài sản
Chúng ta đã nhận diện vai trò của đường CAL để mô tả những sự kết họp sẵn có giữa rủi ro và lợi tức từ những sự lựa chọn phân bổ tài sản khác nhau. Nhà đầu tư bây giờ phải chọn lựa một danh mục đầu tư tối ưu, c, từ tập hợp các danh mục khả thi có sẵn. Sự lựa chọn này chính là sự đánh đổi giữa rủi ro và lợi tức. Các nhà đầu tư cá nhân với các đặc điểm ngại rủi ro khác nhau sẽ lựa chọn để nắm giữ những tỷ trọng khác nhau trong tài sản rủi ro khác nhau. Cụ thể là, những nhà đầu tư càng ngại rủi ro sẽ nắm giữ càng ít tài sản rủi ro và càng nhiều tài sản phi rủi ro.
Trong chương 1, chúng ta đã chỉ ra rằng giá trị hữu dụng mà nhà đầu tư có được từ danh mục đầu tư với một tỷ suất lợi tức kỳ vọng và độ lệch chuẩn có thể được mô tả bằng công thức hàm hữu dụng sau:
ơ = E(R) – 0,005/íơ’
Trong đó, A là hệ số ngại rủi ro. Hàm hữu dụng này diễn tả rằng giá trị hữu dụng của danh mục đầu tư sẽ tăng lên khi tỷ suất lợi tức kỳ vọng tăng lên và sẽ giảm xuống khi phương sai tăng lên. Biên độ cùa những sự thay đổi này được điều chỉnh bởi hệ số ngại rủi ro, A. Với những nhà dầu tư trung tính với rủi ro, thì A = 0. Mức ngại rủi ro càng cao thì giá trị của hệ số ngại rủi ro A càng lớn.
Với một cơ hội đầu tư bao gồm tỷ suất lợi tức phi rủi ro R/Và một danh mục ‘đầu tư rui ro với tỷ suất lợi tức kỳ vọng là E(Rp) và độ lệch chuẩn Op sẽ thấy rằng ứng với bất kỳ một tỷ lệ y nào thì tỷ suất lợi tức mong đợi của DMĐT kết hợp sẽ tuân theo công thức 2.1:
E(RC) = Rf+y[E(Rp) – Rj]
Từ công thức 2.2, phương sai của danh mục đầu tư kết họp là:
ơị = y2ơị
Nhà đầu tư chọn y nhằm tối đa hóa giá trị hữu dụng u. Chúng ta sẽ sử dụng một ví dụ để chỉ rõ tác động của y đối với giá trị hữu dụng cùa nhà đầu tư với A = 4. Theo đó, chúng ta sẽ tính E(RCJ, ơc và ơ sử dụng các công thức từ 2.1 đến 2.3 và công thức 1.18.
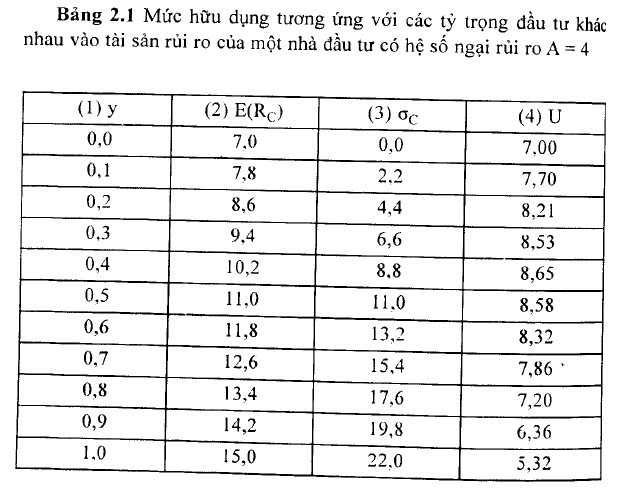
Hình 2.3 biểu diễn hàm hữu dụng từ Bảng 2.1. Hình 2.3 chì ra rằng giá trị hữu dụng cao nhất lại y = 0,41. Khi y < 0,41, các nhà đầu tư sẵn lòng chập nhận nhiều rủi ro hơn để tăng tỷ suất lợi tức kỳ vọng. Nhưng nếu y c~0 hơn. rủi 😮 nhiều hơn, và đầu tư thêm vào tài sản rủi ro là không được ưa chuông; nghĩa là vượt qua điểm này, sự tăng lên của rủi ro sẽ lớn hơn so với gia tăng của tỳ suất lợi tức kỳ vọng và giá trị hữu dụng giảm dần (tuân theo quy luật lợi ích cận biên giảm dần).



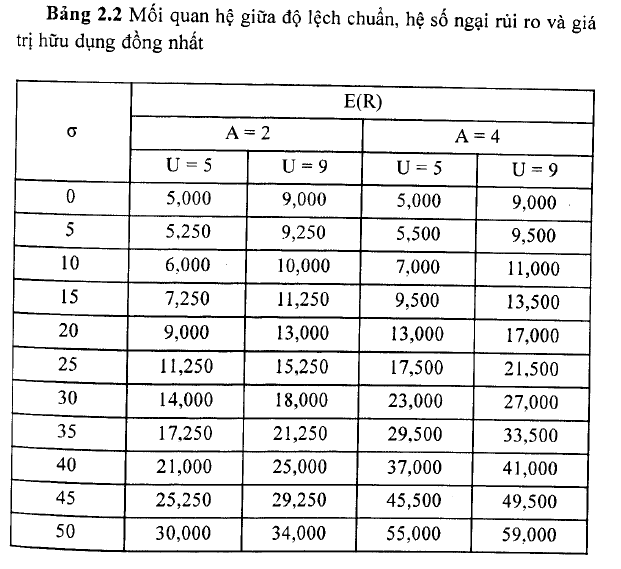
Bởi vì giá trị hữu dụng của danh mục đầu tư phi rủi ro bằng với tỷ suất lợi tức kỳ vọng của danh mục đó, sự giao nhau của những đường cong hữu dụng trong Hình 2.4 (tại mức = 0) được gọi là giá trị chắc chắn tương đương của những DMĐT nằm trên đường cong đó hay nói đúng ra là giá trị hữu dụng của đường cong đó. Trong phần này, thuật ngữ “giá trị chắc chắn tương đương” và “giá trị hữu dụng” có thể thay thế cho nhau. Lưu ý rằng những điểm giao nhau của những đường cong là tại mức 5% và 9%, bằng đúng với giá trị hữu dụng của mỗi đường.
Trên cơ sở những lựa chọn này, bất kỳ nhà đầu tư nào cũng sẽ thích một DMĐT nằm trên đường cong hữu dụng cao hơn (nghĩa là có giá trị chắc chắn tương đương cao hơn). Những danh mục đầu tư nằm trên đường cong hữu dụng cao hơn sẽ mang lại tỷ suất lợi tức kỳ vọng cao hơn ứng với một mức rủi ro được xác định. Trong ví dụ trên, cả hai đường cong hữu dụng của nhà đầu tư với A = 2 có hình dáng giống nhau. Tuy nhiên, danh mục đầu tư với giá trị hữu dụng là 9% mang lại tỷ suất lợi tức kỳ vọng nhiều hơn 4% so với danh mục nằm ở đường cong hữu dụng thấp hơn với u = 5%.
Bảng 2.2 cũng chỉ ra rằng nhà đầu tư càng ngại rủi ro sẽ có đường cong hữu dụng càng dốc hơn. Đường cong hữu dụng dốc hơn nghĩa là nhà đầu tư đòi hỏi một mức tăng tỷ suất lợi tức kỳ cao hơn để bù đắp cho mức gia tăng của rủi ro trong danh mục đầu tư.
Những đường cong hữu dụng đồng nhất cao hơn tương ứng với những mức hữu dụng cao hơn. Do đó, nhà đầu tư sẽ cố gắng tìm một danh mục đầu tư kết hợp nằm trên đường cong hữu dụng cao nhất có thể đạt được. Trên cơ sở đường phân bổ vốn, khi chúng ta đưa thêm càng nhiều những đường cong hữu dụng để tạo ra một tập hợp các cơ hội đầu tư, chúng ta có thể nhận diện được đường cong hữu dụng cao nhất tiếp xúc với đường CAL. Đường cong này là tiếp tuyến với đường CAL và điểm tiếp xúc giữa chúng tương ứng với độ lệch chuẩn và tỷ suất lợi tức kỳ vọng của danh mục đầu tư kết hợp tối ưu.
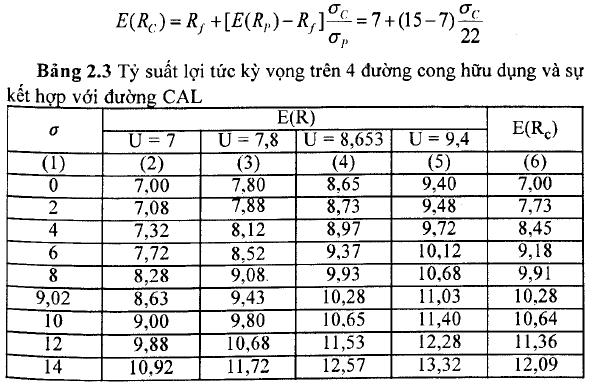
Để mô tả điều này, Bảng 2.3 cung cấp cách thức tính đối với bốn đường cong hữu dụng (với giá trị hữu dụng ở các mức 7%; 7,8%; 8,653% và 9,4%) cho nhà đầu tư có A = 4. Cột (2) đến cột (5) sử dụng công thức 1.18 để tính lợi tức kỳ vọng tương ứng với độ lệch chuẩn ở cột (1), và cho ra giá trị hữu dụng tương ứng với mỗi đường cong. Cột (6) sử dụng công thức 2.3 để tính E(RC) nằm trên đường CAL với độ lệch chuẩn ơc ở cột (1 ):

31 Th12 2020
30 Th12 2020
30 Th12 2020
31 Th12 2020
30 Th12 2020
31 Th12 2020