Đầu tư tài chính
Lý thuyết định giá Arbitrage
Chương trước đã trình bày các cách thức ứng dụng mô hình CAPM trong đầu tư. Xét trên nhiều khía cạnh, mô hình CAPM là một trong những lý thuyết kinh tế tài chính thực sự hữu ích và được sử dụng thường xuyên nhất. Tuy nhiên, nhiều nghiên cứu thực tế đã chi ra một số thiếu sót của mô hình này trong việc giải thích mối quan hệ giữa rủi ro và lợi tức. Chẳng hạn, những kiểm định đối với mô hình CAPM cho thấy rằng hệ số beta của các chứng khoán riêng lẻ không ổn định, trong khi hệ số beta của các danh mục đầu tư thì thường ổn định và tương xứng với khối lượng giao dịch. Bên cạnh đó, đã có thêm nhiều bằng chứng về mối quan hệ tuyến tính giữa tỷ suất lợi tức và rủi ro hệ thống của những danh mục đầu tư chứng khoán. Một vài bằng chứng gần đây cho thấy sự cần thiết phải thêm vào các biến số đại diện cho các rủi to khác. Ngoài ra, một vài nghiên cứu chi trích những tiêu chuẩn và sự hữu dụng của mô hình này trong đậnh giá danh mục đầu tư do sự phụ thuộc của mô hình lên danh mục thị trường.
Một rào cản khác đối với tính hiệu quả của mô hlnh CAPM là một loạt các kết quả thừa nhận rằng có thể sử dụng sự hiểu biết về một công ty nào đó hoặc những đặc trưng của chứng khoán để phát triển chiến lược kinh doanh hiệu quả, thậm chí sau khi điều chỉnh rủi ro đầu tư như đã được đo lường bởi hệ số beta. Điển hinh là những phát hiện của Banz ( 1981 ), cho thấy những danh mục cổ phiếu với giá trị vốn hóa thị trường thấp (những cổ phiếu “nhỏ”) hiệu quà hon là những danh mục đầu tư cổ phiếu “lớn” trên cơ sờ đã điều chinh rủi ro, và Basu (1977), qua quan sát thực nghiệm đã chỉ ra rằng những cổ phiếu có chì số P/E (tỷ lệ giữa giá cồ phiếu và thu nhập) thấp hiệu quả hơn là những cổ phiếu có chỉ số P/E cao. Những nghiên cứu gần đây của Fama và French (1993) cũng chứng minh rằng những cổ phiếu “tăng trưởng” (chẳng hạn như những cổ phiếu có tỷ lệ thị giá trên giá trị sổ sách cao) có khuynh hướng đem lại tỷ suất lợi tức đã được điều chỉnh rủi ro lớn hơn so với những cổ phiếu “giá trị” (những cổ phiếu có tỷ lệ thị giá trên giá trị sổ sách thấp). Tất nhiên, toong một thị trường hiệu quả, những chênh lệch về lợi tức thường ít khi xảy ra, mà chỉ xảy ra một trong hai tổng kết sau đây: (1) Các thị trường không hoạt động hiệu quả trong những giai đoạn mở rộng của thời kỳ dầu tư (nhà đầu tư không quan tâm đến những cơ hội đầu tư có hiệu quả trong nhiều thập niên), hoặc (2) Giá cả thị trường được hình thành hợp lý nhưng có gì đó không đúng trong cách đo lường rủi ro của các mô hình nhân tố đơn như mô hình CAPM.
Lý thuyết kinh doanh chênh lệch giá Arbitrage (APT – Arbitrage Pricing Theory) đã được Ross đề xuất vào khoảng giữa thập niên 70 của thế kỷ 20. Theo lý thuyết này, mối quan hệ TSLT mong đợi – rủi ro có thể được giải thích như sau: Nếu hai sự đầu tư hoàn toàn giống nhau và có TSLT kỳ vọng khác nhau thì một nhà đầu tư có thể đạt được lợi nhuận phi rủi ro bằng việc mua sự đầu tư với TSLT mong đợi cao hơn và bán khống sự đầu tư có TSLT mong đợi thấp hơn. Khi TSLT của các chứng khoán có cùng hệ số beta nhung TSLT khác nhau thỉ sẽ tạo ra cơ hội kinh doanh chênh lệch giá.
1. Các giả định của Lý thuyết định giá Arbitrage
Lý thuyết định giá Arbitrage dựa vào ba giả định chính:
- Các tỷ suất lợi tức có thể được mô tả bằng một mô hình nhân tố, và quá trình hình thành tỷ suất lợi tức của tài sản có thể được biểu diễn bởi một hàm tuyến tính được xác lập từ K nhân tố rủi ro.
- Thị trường vốn là thị trường cạnh tranh hoàn hảo và vì thế không tồn tại các cơ hội chênh lệch giá.
- Có một số lượng lớn các chứng khoán, vì thế có thể thiết lập các DMĐT đa dạng hóa rủi ro đặc thù của từng loại chứng khoán riêng lẻ.
Trước khi thảo luận về những kiểm định thực nghiệm của APT, chúng ta sẽ tìm hiểu những vấn đề cơ bản nhất của mô hình APT. Như đã đề cập ở trên, lý thuyết này giả định rằng quá trình hình thành ngẫu nhiên lợi tức của tài sản có thể được biểu diễn bởi một mô hình có K nhân tố, cụ thể:

Nói một cách ngắn gọn, F là tập hợp những nhân tố rủi ro có sự tác động đến tỷ suất lợi tức của toàn bộ tài sản đầu tư trong danh mục, như lạm phát, tốc độ tăng trường GDP, sự thay đổi chính sách của chính phủ, hoặc sự thay đổi của lãi suất. Lý thuyết APT cho rằng có rất nhiều nhân tố rủi ro như thế ảnh hưởng đến tỷ suất lợi tức, trái ngược với CAPM chỉ có một nhân tố rủi ro liên quan để đo lường, đỏ là hiệp phương sai giữa một chứng khoán với danh mục đầu tư thị trường (hệ số beta của chứng khoán đó).
Căn cứ vào những nhân tố chung, các ậịị cho biét độ nhạy của tài sản i khi có sự ảnh hường của nhân tố rủi ro thứ j. Chẳng hạn, theo kinh nghiệm thực tế gần đây, hầu như toàn bộ chứng khoán đều có thể bị ảnh hưởng bởi sự tăng trưởng của GDP, tuy nhiên sự tác động đó đến mỗi chứng khoán sẽ là khác nhau. Ví dụ, những cổ phiếu của các công ty có tính chu kỳ thì chịu ảnh hưởng bởi sự tăng trưởng GDP lớn hơn là những cổ phiếu của các công ty không có tính chu kỳ. Tương tự với độ nhạy theo lãi suất của cổ phiếu. Tất cả cổ phiếu đều bị ảnh hưởng bởi sự thay đổi của lãi suất với những mức độ không như nhau. Ví dụ, một cổ phiếu nhạy cảm với lãi suất có hệ số ßj > 2, ứong khi một cổ phiếu tương đối không nhạy với lãi suất có hệ số ßj = 0,5. Những ví dụ khác về những nhân tố rủi ro phổ biến khác như sự thay đổi tỷ lệ thất nghiệp, tỷ giá hối đoái, sự biến thiên của đường cong lợi tức.
Tương tự như mô hình CAPM, APT cũng giả định rằng các £j là độc lập và sẽ bằng 0 một khi danh mục đầu tư được đa dạng hóa. Một cách cụ thể, APT yêu cầu trong điều kiện thị trường cân bằng, tỷ suất lợi tức của những danh mục đầu tư phi rủi ro là bằng 0 khi £,= 0. Như vậy, E(Rị) cũng có thể được biểu diễn như sau:

Phương trình cùa Lý thuyết APT, phương hình (4.4), thể hiện mối quan hệ giữa rủi ro và TSLT kỳ vọng mà không có các cơ hội chênh lệch, vế trái của phương trình là TSLT kỳ vọng của một sự đàu tư. vế phải là TSLT kỳ vọng của một DMĐT mô phỏng với cùng các ß nhân tố của sự đầu tư. Phương trình (4.4) chỉ ra rằng nếu 02 tài sản hay 02 danh mục đầu tư có hệ số beta bằng nhau, tỷ suất lợi tức kỳ vọng của 02 tài sản hay danh mục đầu tư này sẽ bằng nhau. Nếu không, nhà đầu tư sẽ tiến hành kinh doanh chênh lệch giá và điều này sẽ làm cân bằng tỷ suất lợi tức của 02 tài sản này.
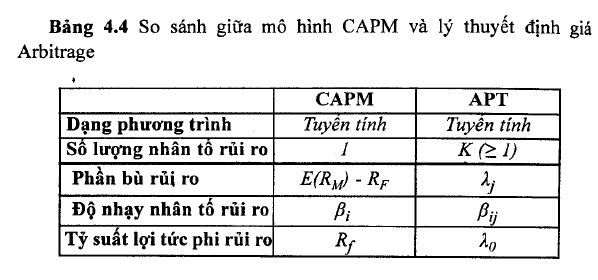
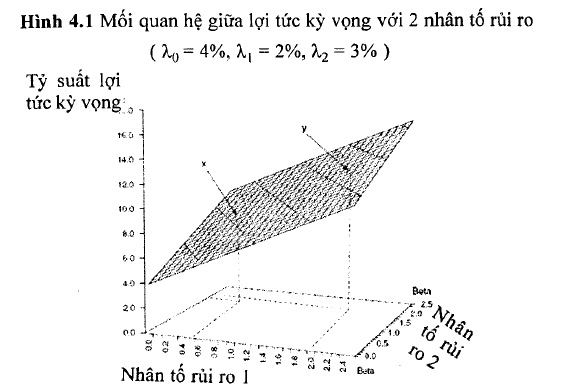
Bảng 4.4 trên đây tổng hợp những đặc tính có liên quan của hai mô hình này. Từ bảng tóm tắt này, ta nhận thấy một cách rõ ràng sự khác nhau cơ bản giữa hai lý thuyết trên nằm trong cách xác đinh rủi ro hệ thống, cụ thể một vài nhân tố rủi ro phản ánh rõ hơn những đặc điểm thị trường so với chỉ một nhân tố rủi ro đơn như sử dụng trong mô hình CAPM. Điều quan trọng phải nhận thấy là cả hai lý thuyết trên đều dựa vào những mô hình tuyến tính trên cơ sở tin tưởng rằng những nhà đầu tư sẽ được bù đắp từ việc thực hiện hai chức năng: điều chuyển vốn và chấp nhận rủi ro. Cuối cùng, lưu ý rằng phương trình APT đưa ra giả thiết về một mối liên hệ tương tự như đường thị trường chứng khoán của CAPM. Tuy nhiên, thay vì kết hợp giữa rủi ro và lợi tức kỳ vọng, APT sử dụng một mặt phăng không gian thị trường chứng khoán với kích thước (K+l) chiều, trong đó K là chiều biểu diễn cho K nhân tố rủi ro và 1 chiều thêm vào biểu diễn cho tỷ suất lợi tức kỳ vọng của chứng khoán. Hình 4.1 minh họa cho mối quan hệ của hai nhân tố rủi ro (K~2).
2. Mô hình APT một nhân tố và đa dạng hóa danh mục đầu tư
Stephen Ross đã phát triển lý thuyết định giá Arbitrage vào năm 1976. Chúng ta bắt đầu bằng cách thảo luận một phiên bản đon giản của mô hình, mà giả sử rằng chỉ có một nhân tố hệ thống tác động đến lợi tức chứng khoán, mặc dù mô hình APT liên quan đến đa nhân tố tác động.
Ross bắt đầu bằng cách khảo sát mô hlnh một nhân tố. Theo mô hỉnh này, sự không chắc chắn trong lợi tức của tài sản bắt nguồn từ 2 lý do: nhân tố chung hay nhân tố kinh tế vĩ mô, và một nguyên nhân xuất phát từ đặc trưng của doanh nghiệp. Nhân tố chung được giả định rằng giá trị kỳ vọng bằng 0, bởi vì nỏ đo lường các thông tin mới liên quan đến nền kinh tế vĩ mô (theo quy ước, nhân tố kinh tế vĩ mô có giá trị ước lượng bằng 0).
Nếu gọi F là độ lệch của các nhân tố chung so với giá trị kỳ vọng của nó, ßi là hệ số đo lường độ nhạy của công ty i đối với nhân tố chung, eị là đặc điểm riêng có của công ty, mô hình nhân tố xác nhận rằng lợi tức thực tế của công ty i bằng lợi tức kỳ vọng ban đầu cộng với phần lợi tức ngẫu nhiên được tạo ra do sự thay đổi của các nhân tố vĩ mô, và cộng với phần lợi tức ngẫu nhiên được tạo ra do sự thay đổi của cácyihân tố riêng cỏ của công ty.

Đa dạng hóa danh mục đầu tư
Quan sát rủi ro của một danh mục cổ phiếu. Nếu danh mục được đa dạng hóa tốt, các yếu tố thuộc đặc điểm riêng công ty hay rủi ro phi hệ thống cũng có thể được đa dạng hóa hoàn toàn (có thể được loại trừ). Chi có các nhân tố rủi ro hệ thống là không thể loại bỏ. Cho n chứng khoán trong danh mục đầu tư với tỷ trọng là Wj, biét 2w¡= 1. Tỷ suất lợi tức sẽ được xác định bởi công thức:


Trong trường hợp này, chúng ta chia phương sai bình quân phi hệ thống cho n. Do đó, khi danh mục đầu tư được mở rộng (n lớn) và tỷ trọng các cổ phiếu bằng nhau, thì phương sai phi hệ thống sẽ gần bằng 0.
Danh mục đầu tư được đa dạng hóa tốt là một danh mục đầu tư tập hợp được các chứng khoán đủ lớn với tỷ lệ mỗi chứng khoán là wi và phương sai phi hệ thống, ơ2(ep), là không đáng kể.
Bởi vì giá trị kỳ vọng của ep là bằng 0, nếu phương sai của ep cũng bằng 0, chúng ta có thể kết luận rằng bất kỳ giá trị thực tế nào của ep cũng hầu như là bằng 0. Theo công thức 4.4, chúng ta có thể kết luận rằng, một danh mục đầu tư được đa dạng hỏa sẽ là:
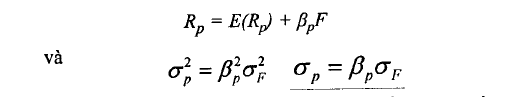
Nhà đầu tư lớn có thể nắm giữ danh mục đầu tư bao gồm hàng trăm hoặc thậm chí hàng ngàn cổ phiếu; như vậy khái niệm đa dạng hóa danh mục đầu tư rõ ràng là kỹ thuật nghiệp vụ trong thị trường tài chính hiện đại. Tuy nhiên, đa dạng hóa danh mục đầu tư không nhất thiết là tỳ trọng của các tài sản trong danh mục đầu tư phải bằng nhau.
Xem xét một danh mục đầu tư bao gồm 1.000 cổ phiếu. Già định tỷ trọng của chứng khoán thứ nhất là w%, chứng khoán thứ 2 là 2w%, chứng khoán thứ 3 là 3w%,… Theo cách này, chứng khoán có tỳ trọng lớn nhất sẽ là 1.000w%. Có hay không danh mục đầu tư này cũng được đa dạng hóa tốt khi mà thực tế chủng khoán thứ 1.000 có tỷ trọng lớn gấp 1.000 lần chứng khoán đầu tiên. Và, câu trả lời là có.
Nhận thấy rằng tỷ trọng lớn nhất trong tất cả các cổ phiếu trong trường hợp này là chứng khoán thứ 1.000. Mà tổng tỷ trọng của các cổ phiếu phải là 100%, do đó:
w + 2w +……… +1000w = 100%
Chúng ta tính ra được:
w = 0,0002% 1000w = 0,2%
Tỷ trọng lớn nhất chỉ có 0,2%. Và đây là một con số rất khác xa so với danh mục có tỷ trọng cân bằng. Tuy nhiên, đây vẫn là một danh mục được đa dạng hóa hiệu quả.
Hệ số Beta và lợi tức kỳ vọng
Do rủi ro phi hệ thống có thể được đa dạng hóa, chi có rủi ro hệ thống là yêu cầu một phần bù rủi ro trong cân bằng thị trường. Rủi ro phi hệ thống của các công ty có thể được loại bỏ trong một danh mục đầu tư được đa dạng hóa hiệu quả, do đó chi có rủi ro hệ thống của các chứng khoán trong danh mục đầu tư là có liên quan tới tỷ suất lợi tức kỳ vọng.
Đường in đậm trong Hình 4.2A diễn tả tỷ suất lợi tức của danh mục đầu tư được đa dạng hóa hiệu quả với ßA = 1. Tỷ suất lợi tức thực tế của danh mục A là 10% tại điểm mà đường in đậm này cắt trục tung. Tại điểm này, các nhân tố hệ thống là bằng 0, nghĩa là không có sự thay đổi của các yếu tố vĩ mô. Nếu nhân tố vĩ mô thay đổi theo hướng tích cực, tỷ suất lợi tức của danh mục đầu tư sẽ vượt quá giá trị kỳ vọng của nỏ. Ngược lại, tỷ suất lợi tức của danh mục sẽ thấp hơn giá trị kỳ vọng. Do đó, tỷ suất lợi tức của danh mục sẽ là:
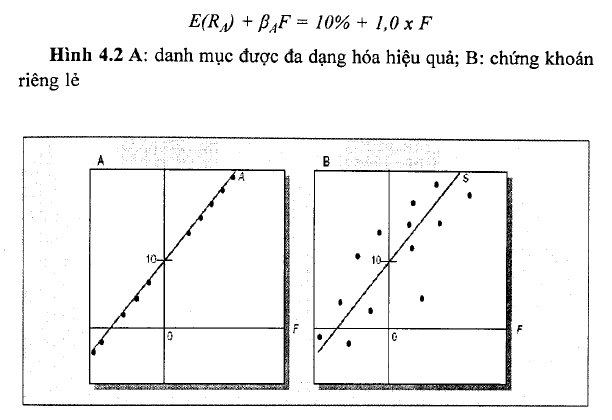
So sánh Hình 4.2A với 4.2B, danh mục A và chứng khoán B đều có ß = 1 của một cổ phiếu đơn nhất. Chứng khoán không đa dạng hóa sẽ đối mặt với rủi ro phi hệ thống. Đây là những điểm phân tán xung quanh đường in đậm. Ngược lại, lợi tức của danh mục đầu tư được đa dạng hóa hiệu quả được quyết định bởi các nhân tố hệ thống.
Bây giờ xem xét Hình 4.3, đường đứt nét biểu diễn lợi tức của một danh mục đầu tư được đa dạng hóa hiệu quả khác, B, với tỷ suất lợi tức kỳ vọng là 8% và ßB gần bằng 1. vấn đề là có hay không danh mục A và B cùng tồn tại với những tỷ suất lợi tức như đã được đề cập. Rõ ràng là không. Bất kể các nhân tố hệ thống biến động như thế nào, danh mục A vẫn tốt hơn danh mục B, và tạo ra một cơ hội Arbitrage.

Nhà đầu tư có được lợi tức phi rủi ro này là bởi vì các yếu tố rủi ro đã bị hủy bỏ trong quá trình mua – bán đồng thời, tất nhiên giá trị đầu tư ròng phải bằng 0. vấn đề là ở chỗ nhà đầu tư phải liên tục thiết lập các trạng thái khác nhau cho đến khi sự khuếch tán lợi tức giữa 2 danh mục đầu tư biến mất. Những danh mục đầu tư đa dạng hóa tốt với hệ số ß bằng nhau phải có lợi tức kỳ vọng bằng nhau khi thị trường cân bằng.
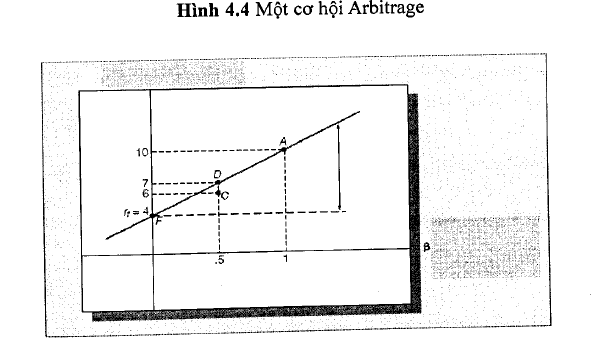
Vậy điều gì sẽ xảy ra nếu hệ số beta khác nhau? Chúng ta sẽ chỉ ra rằng phần bù rủi ro của chúng phải tương xứng với hệ số beta. Xem xét Hình 4.4. Giả định rằng lợi tức phi rủi ro là 4% và rằng danh mục c được đa dạng hóa hiệu quả với hệ số ß là 0,5 và lợi tức kỳ vọng là 6%. Xem xét thêm một danh mục mới, D, gồm một nửa là danh mục A và một nửa là tài sản phi rủi ro. Hệ số ß của danh mục D sẽ là (1/2 X 0 + 1/2 X 1,0)= 0,5 và lợi tức kỳ vọng là (1/2 X 4 + 1/2 X 10 ) = 7%. Danh mục D lúc này có hệ số ß bằng danh mục c, nhưng cỏ lợi tức kỳ vọng lớn hơn danh mục c. Điều này tạo ra cơ hội Arbitrage.
Như vậy, tất cả các danh mục đầu tư được đa dạng hóa hiệu quả phải nằm trên đường thẳng bắt nguồn từ điểm gốc là tài sản phi rủi ro.
Chú ý trong Hình 4.4 rằng những phần bù rủi ro tỷ lệ tương ứng với những hệ số beta của danh mục đầu tư. Phần bù rủi ro được biểu diễn bởi trục tung để đo lường chênh lệch giữa lợi tức phi rủi ro và lợi tức kỳ vọng của danh mục đầu tư. Phần bù này sẽ bằng 0 khi hệ số beta bằng 0, và tăng với tỷ lệ tương xứng với sự thay đổi của hệ số beta.
Giả sử rằng hai danh mục được đa dạng hóa hiệu quả được kết hợp với nhau thành một danh mục z có hệ số ß bằng 0. Tất nhiên các tông các quyền số của hai tài sản trong danh mục z bằng 1, và hệ sô ß của danh mục là 0.

Danh mục z là danh mục phi rủi ro. Nó không tiềm ẩn rủi ro phi hệ thống bởi vì đã được đa dạng hóa hiệu quả, và cũng không tồn tại rủi ro hệ thống bởi vì hệ số ß bằng 0. Khi đỏ, nếu không tồn tại cơ hội kinh doanh chênh lệch giá, lợi tức của danh mục phải là lợi tức phi rủi ro. Vì vậy:
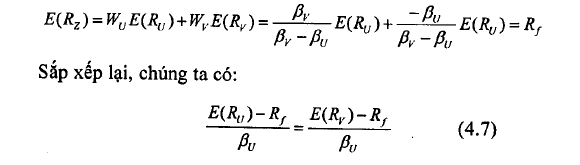
Phương trình này hàm ý rằng những phần bù rủi ro tỷ lệ tương ứng với những hệ số beta (như đã được đề cập trong Hình 4.4)
3. Lý thuyết định giá Arbitrage và đường thị trường chứng khoán (SML)
Hãy xem xét danh mục thị trường như là một danh mục được da dạng hóa hiệu quả và việc đo lường rủi ro hệ thống dựa trên cơ sở xác định sự biến thiên lợi tức trên danh mục thị trường. Bởi vì danh mục thị trường phải nằm trên đường thẳng trong Hỉnh 4.4 và có ß bằng 1, chúng
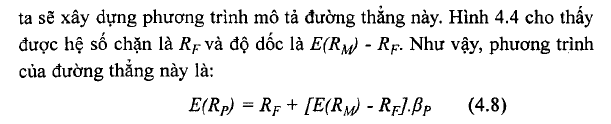
Chúng ta đã sử dụng những điều kiện không có Arbitrage để có được quan hệ ß – lợi tức kỳ vọng giống với mô hình CAPM, nhưng không có sự áp đặt của các giả định trong CAPM.
Ngược với mô hình CAPM, mô hình APT không yêu cầu rằng danh mục đầu tư tối ưu nằm trên đường SML phải là danh mục thị trường. Bất kỳ danh mục được đa dạng hiệu quả nằm trên đường SML của Hình 4.4 đều có thể là danh mục tối ưu. Chẳng hạn, chúng ta có thể định nghĩa đanh mục đầu tư tối ưu như là một danh mục được đa dạng hóa hiệu quả và có mối tương quan cao nhất với các nhân tố hệ thống (yếu tố được kỳ vọng là sẽ ảnh hưởng đến lợi tức chứng khoán). Theo đó, APT có nhiều ưu điểm hơn CAPM do không cần sử dụng đến danh mục thị trường, một danh mục không quan sát được.

31 Th12 2020
31 Th12 2020
31 Th12 2020
31 Th12 2020
31 Th12 2020
30 Th12 2020