Đầu tư tài chính
Mô hình APT và CAPM
APT là mô hình khá hữu ích. Mô hình này dựa vào giả thiết không tồn tại cơ hội Arbitrage. Chỉ cần một sự vi phạm giá xuất hiện, kinh doanh chênh lệch giá sẽ làm cân bằng giá trở lại ngay cả khi chỉ có một số lượng hạn chế nhà đầu tư.
Hơn nữa, APT phản ánh mối quan hệ tỷ suất lợi tức kỳ vọng – beta sử dụng danh mục đầu tư được đa dạng hóa hiệu quả được xây dựng từ một số lượng lớn chứng khoán. Ngược lại, CAPM bắt nguồn từ giả định tồn tại một danh mục “thị trường” vốn dĩ khó quan sát được trong thực tế. Mặc dù có những lợi thế này, mô hình APT cũng không hoàn toàn vượt trội so với CAPM. CAPM cung cấp một mối quan hệ khá phi thực tế giữa lợi tức kỳ vọng và hệ số beta đối với tất cả các tài sản tài chính. Trong khi đó, APT cũng ám chỉ đến mối quan hệ này, nhưng đối với một số lượng giới hạn các chứng khoán. Đây là một sự khác biệt quan trọng, tuy nhiên không có nhiều ý nghĩa vì mô hình CAPM là mô hình khó có khả năng kiểm định ngay. Vì thế, hầu hết các nhà nghiên cứu thường so sánh giữa APT và mô hình chỉ số đơn (SIM).
Nhớ lại rằng mô hình SIM dựa trên mô hình CAPM với các giả định thêm rằng: (1) chi số thị trường có tương quan hoàn hảo vớỉ danh mục thị trường; và (2) hàm phân phối xác suất của lợi tức cổ phiếu là không thay đổi trong một khoảng thời gian nhất định và cho phép ước tính về lợi tức kỳ vọng và phương sai.
Cơ sở của mô hình Chỉ số đơn là danh mục chỉ số thị trường là hiệu quả và rằng quan hệ ß – tỷ suất lợi tức kỳ vọng tồn tại đối với tất cả tài sản. Các giả định về tính ổn định của hàm phân phối xác suất và sự quan sát được của chi số thị trường làm cho mô hình này dễ dàng tính toán được tính hiệu quả của danh mục thị trường cũng như mối quan hệ lợi tức kỳ vọng – beta.
Ngược lại, APT sử dụng lý thuyết nhân tố để đánh giá mối quan hệ tỷ suất lợi tức kỳ vọng – beta của danh mục được đa dạng hỏa hiệu quả. Bởi vì APT tập trung vào điều kiện không tồn tại Arbitrage, và không có thêm giả định khác như mô hình chỉ số đơn, APT hầu như không vi phạm quan hệ ß – tỷ suất lợi tức kỳ vọng đối với bất kỳ tài sản cụ thể nào.
Như đã đề cập ở trên, thách thức chủ yếu khi sử dụng APT trong định giá chứng khoán liên quan đến việc nhận diện các nhân tố rủi ro. Phần này minh họa cách thức thực hiện mô hình APT thông qua việc già định rằng có hai nhân tố rủi ro: một nhân tố liên quan đến những thay đổi không mong đợi của tỷ lệ lạm phát, nhân tố còn lại liên quan đến những thay đổi không dự báo trước của GDP. Nếu ta giả định thêm rằng phần bù rủi ro liên quan đến độ nhạy của GDP là 0,03 và một cổ phiếu nhạy cảm với GDP có hệ số bj =1,5 (j là nhân tố GDP), điều này nghĩa là nhân tố GDP làm cho tỷ suất lợi tức kỳ vọng của cổ phiếu tăng lên 4,5% (= 1,5 X 0,03).
Để phát triển lý thuyết này, ta hãy xem xét một ví dụ gồm 2 cổ phiếu và một mô hình 2 nhân tố. Đầu tiên, xem xét mỗi nhân tố rủi ro và độ nhạy của chúng:

Độ nhạy của những nhân tố này có thể hiểu gần giống như hệ số ß trong mô hình CAPM. Điều này có nghĩa là hệ số bụ càng cao thi độ nhạy của cổ phiếu i đối với sự thay đổi của nhân tố rủi ro j càng lón. Theo đó, những hệ số đo lường độ nhạy trên cho thấy rằng nểu những nhân tố chủ yếu trên ảnh hưởng đến lợi tức của cổ phiếu, thì cổ phiếu Y có rủi ro cao hơn cổ phiếu X, và đương nhiên lợi tức kỳ vọng của cổ phiếu Y sê lớn hơn. Phương trình tổng quát của lợi tức kỳ vọng sẽ là:
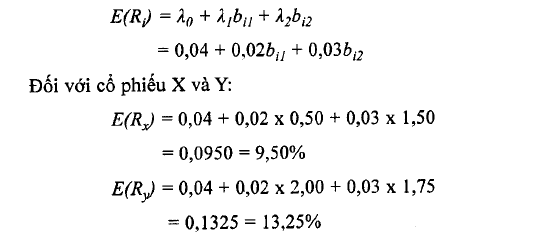
Nếu giá của 2 cổ phiếu trên không phản ánh đúng những tỷ suất lợi tức kỳ vọng này, khi đó nhà đầu tư sẽ tham gia vào các nghiệp vụ Arbitrage bời nhờ đó họ sê bán những cổ phiếu được định giá cao trong ngắn hạn và sử dụng số tiền thu được trên để mua những cổ phiếu định giá thấp cho đén khi các mửc giá được xác định chính xác ừở lại. Căn cỏ vào các mối quan hệ tuyến tính này, ta có thể tìm được một cổ phiếu hoặc một danh mục kết hợp nhiều cổ phiếu có cùng một mức rủi ro với cổ phiếu bị định giá sai, song lại có một mức tỷ suất lợi tức kỳ vọng cao hơn. Phần tiếp theo cung cấp một ví dụ chi tiết về việc sử dụng APT trong quá trình định giá chứng khoán.

31 Th12 2020
31 Th12 2020
16 Th1 2018
30 Th12 2020
31 Th12 2020
31 Th12 2020