Đầu tư tài chính
Đo lường tỷ suất lợi tức
1. Đo lường tỷ suất lợi tức quá khứ
Khi đánh giá giữa các cơ hội đầu tư, nhà đầu tư thông thường so sánh những cơ hội đầu tư này với sự biến động giá trên thị trường. Chẳng hạn, nhà đàu tư muốn so sánh giữa một cổ phiếu giá 30.000 đồng không được trả cổ tức với cổ phiếu giá 150.000 đồng trả cổ tức 5.000 đồng/năm. Để định giá hợp lý hai cơ hội đầu tư này, cần phải so sánh một cách chính xác tỷ suất lợi tức quá khứ của hai cổ phiếu đó.
Khi chúng ta đầu tư, chúng ta trì hoãn tiêu dùng hiện tại nhằm tăng thêm giá trị phục vụ cho việc tiêu dùng nhiều hơn trong tương lai. Bởi vậy, khi chúng ta nói về thu nhập của một hoạt động đầu tư, chúng ta sẽ quan tâm đến kết quả thay đổi của tài sản từ sự đầu tư. Sự thay đổi trong giá trị tài sản này có thể do dòng tiền vào như tiền lãi hay cổ tức hoặc có thể tạo ra bởi sự thay đổi thị giá của tài sản (tăng hoặc giảm).
Nếu chúng ta bỏ ra 200 triệu đồng để đàu tư vào cổ phiếu VNM tại thời điểm đầu năm và nhận lại được 220 triệu đồng vào thời điểm cuối nãm. Tỷ suất lợi tức trong khoảng thời gian này là bao nhiêu? Khoảng thời gian thực hiện hoạt động đầu tư đó gọi là thời gian nam giữ (holding period) và thu nhập nhận được trong khoảng thời gian đó gọi là thu nhập hay lợi tức thời kỳ (holding period return – HPR), Trong ví dụ trên, HPR được tính như sau:
HPR = Giá trị lúc kết thúc khoản đầu tư /Giá trị lúc bắt đầu khoản đầu tư (1.1)
= 220 triệu/200 triệu =1,10
Giá trị này sẽ luôn luôn bằng hoặc lởn hơn 0, và không bao giờ nhận giá trị âm. Khi giá trị này lớn hơn 1 (HPR>1), nghĩa là giá trị tài sản tăng, tức là nhà đầu tư nhận được một tỷ suất lợi tức dương trong suốt thời gian đầu tư. Ngược lại, khi giá trị này nhỏ hơn 1 (HPR<1), nghĩa là giá trị tài sản bị sụt giảm, và nhà đầu tư nhận được lợi tức âm trong suốt thời kỳ đầu tư. Khi HPR=0, nghĩa là nhà đầu tư đã đánh mất hết tiền của mình.
Mặc dù HPR giúp chúng ta ước tính được sự thay đổi trong giá trị của hoạt động đầu tư, nhà đầu tư thông thường ước tính thu nhập theo tỷ lệ phần trăm. Sự chuyển đổi này tạo điều kiện dễ dàng để so sánh giữa những cơ hội đầu tư thay thế một cách trực tiếp, vì nó cho phép chỉ ra các điểm khác biệt một cách rõ ràng. Để biến đổi HPR sang tỷ lệ phần trăm, ta tính tỷ suất lợi tức thời kỳ (holding period yied – HPY). HPY sẽ bằng HPR trừ 1.
HP Y = HPR -1 (1.2)
Trong ví dụ của ở trên:
HPY = 1,1 – 1 = 0,1 hay 10%
Ở một khía cạnh liên quan, thông thường nhà đầu tư cần xác định tỷ suất lợi tức trên cơ sở năm, gọi là tỷ suất lợi tức hàng năm (Annual Holding Period Yied – AHPY)7
AHPY = é + HPY-l (1.3) trong đó, n là số năm đầu tư.
Ví dụ 1.1: Xem xét một cơ hội đầu tư vào chứng khoán với tổng giá trị vốn bỏ ra ban đầu là 500 triệu đồng và được định giá là 1,2 tỷ đồng sau 2 năm nắm giữ:
HPR = Giá trị ban đầu của khoản đầu tư/Giá trị kết thúc khoản đầu tư

Chú ý là chúng ta có một số giả thiết khi chuyển đổi ra AHPY. Cụ thể, tỷ suất lợi tức hằng năm được giả định không đổi cho mỗi năm. Ở ví dụ đầu tiên (khoảng thời gian 2 năm đầu tư), chúng ta giả sử tỷ suất lợi tức là 54,92% mỗi năm. Ờ ví dụ thứ hai (thời gian nắm giữ chi trong 6 tháng), chúng ta giả sử rằng tỷ suất lợi tức được cộng dồn cho cả năm. Nói cách khác, chúng ta giả sừ rằng tỷ suất lợi tức kiếm được ở 6 tháng đầu của năm cũng tương tự như giá trị ở 6 tháng còn lại. Đẻ dễ dàng đánh giá lợi tức từ đầu tư, tỷ suất lợi tức thường được quy đổi theo năm, chúng ta sử dụng công thức tính lãi kép cho các mức lợi tức trong một năm. Theo đó, 12% tỷ suất lợi tức của 6 tháng đầu sẽ được tính theo phương pháp lãi kép để hình thành mức 25,44% tỷ suất lợi tức cho toàn năm. Thực tế, bời vì sự không chắc chắn của việc kiếm được một khoản lợi tức tương tự trong 6 tháng tiếp theo, các định chế (chẳng hạn như các ngân hàng thương mại) sẽ không tính theo lãi kép các dòng thu nhập từng phần trong năm.
Một điểm cần lưu ý là giá trị kết thúc của khoản đầu tư có thể là kết quả của sự tăng hoặc gỉảm của: (i) giá trị tài sản đầu tư (chẳng hạn, một cổ phiếu có giá tăng từ 15.000 đồng lên 20.000 đồng), (ii) thu nhập từ sự đầu tư, (iii) hoặc kết hợp giữa sự thay đổi giá và thu nhập. Giá trị cuối cùng bao gồm giá trị của tất cả các khoản thu liên quan đến hoạt động đầu tư.
Vì thế công thức tổng quát của HPY là:
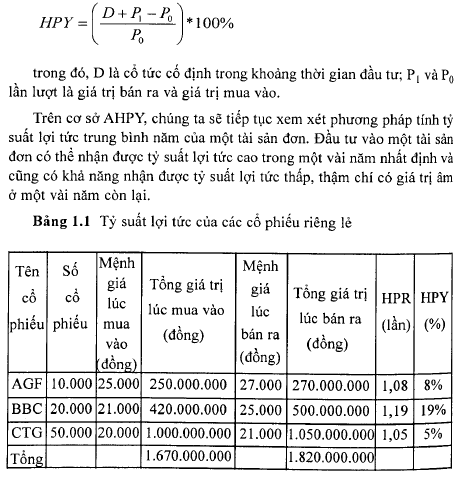
Với một chuỗi tỷ suất lợi tức hằng năm (AHPYs) đối với một tài sản đơn đã biết, có 02 phương pháp đo lường tỷ suất lợi tức trung bình năm. Thứ nhất là phương pháp trung bình cộng (Arithmetic Mean – AM), và thứ hai là phương pháp trung bình nhân (Geometric Mean – GM).
Tỷ suất lợi tức năm theo phương pháp trung bình cộng (AM) sẽ bằng tổng các AHPY hằng năm chia cho tổng số năm đầu tư (n):

Để minh họa cho những phương pháp tính ở trên, chúng ta xem xét một cơ hội đầu tư vào cổ phiếu FPT với những dữ liệu sau:
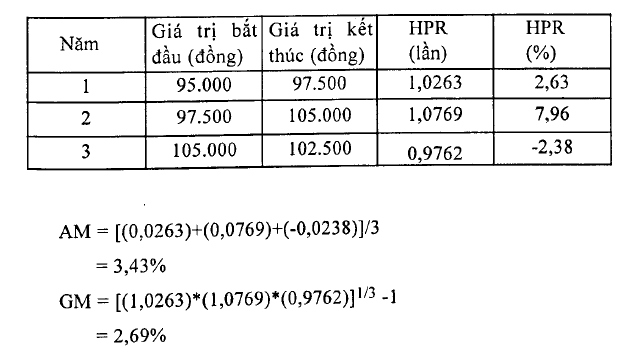
Nhà đầu tư thường quan tâm đến hoạt động đầu tư dài hạn khi so sánh giữa những cơ hội đầu tư thay thế. GM được xem là phương pháp tốt nhất để đo lường tỷ suất lợi tức trung bình dài hạn vì nó thể hiện tỷ suất lợi tức kép hằng năm dựa trên sự so sánh giá trị lúc bán ra và giá trị lúc mua vào của tài sản. Chẳng hạn, nếu chúng ta tính theo phương pháp lãi kép của tỷ suất 2,69% cho 3 năm, tức (1,0269)3, chúng ta nhận được giá trị cuối cùng là 1,082. Như vậy, lãi suất kép cộng dồn trong khoảng thời gian 3 năm lên đến 8,2% thay vì đơn thuần là 1,0269*3 = 8,07%.
Ngược lại, tỷ suất lợi tức trung bình cộng thể hiện thành quả tiêu biểu (mang tính đại diện) cho một năm cụ thể. Mặc dù phương pháp trung bình cộng giải thích tốt tỷ suất lợi tức kỳ vọng đối với một hoạt động đầu tư cho một năm cụ thể, nó thường bị lượng hóa quá cao nếu được dùng để đo lường giá trị của tài sản trong dài hạn. Điều này càng rõ ràng đối với một chứng khoán biến động mạnh.
Xem xét ví dụ, cổ phiếu Công ty cổ phần Sữa Việt Nam (VNM) tăng giá từ 120.000 đồng lên 240.000 đồng trong năm đầu tiên niêm yết và giảm giá xuống còn 120.000 đồng trong năm thứ 2. Tỷ suất lợi tức trung bình hàng năm sẽ là:

Kết quả theo phương pháp GM rõ ràng cho thấy không có sự thay đổi giá trị tài sản qua 2 năm đầu tư. Trong khi đó, ở phương pháp AM, tỷ suất bình quân năm lên đến 25%.
Nếu tỷ suất lợi tức thay đổi qua các năm thì GM sẽ luôn nhỏ hơn AM. Sự khác biệt về giá trị trung bình giữa hai phương pháp phụ thuộc vào sự thay đổi của tỳ suất lợi tức hằng năm. Tỷ suất lợi tức hằng năm biến động càng lớn thì sự chênh lệch trong giá trị giữa 2 phương pháp cũng càng lớn.
2. Đo lường tỷ suất lợi tức kỳ vọng
Trái với tỷ suất lợi tức quá khứ, nhà dầu tư trong trường hợp này kỷ vọng vào triển vọng của một cơ hội đầu tư thông qua tỷ suất lợi tức kỳ vọng. Chẳng hạn, khi nhà đầu tư ước đoán cơ hội đầu tư đem lại tỷ suất lợi tức 10%, con số này thể hiện sự ước tính tốt nhất của nhà đầu tư (được gọi là điểm irớc tính). Nói cách khác, nhà đầu tư có thể biết rõ sự không chắc chắn của tỳ suất lợi tức kỳ vọng và chấp nhận rằng dưới những điều kiện nhất định, tỷ suất lợi tức thấp nhất hằng năm có thể nhận giá trị âm, chẳng hạn -10%, và cũng có thể tăng trưởng cao nhất lên đến, chẳng hạn 25%. Điểm ước tính kỳ vọng này được xác định từ một chuỗi các lợi tức có thể xảy ra từ hoạt động đầu tư và phản ánh sự không chắc chắn của thu nhập thực tế. Chuỗi các lợi tức này càng rộng thì cơ hội đầu tư càng rủi ro.
Nhà đầu tư tính toán tỷ suất lợi tức kỳ vọng bằng cách phân tích các tỷ suất ước tính. Để làm được điều này, nhà đầu tư phải ấn định tất cả các khả năng (xác suất) có thể xảy ra cùa tất cà các mức lợi tức. Những giá trị xác suất này thay đổi từ 0 (nghĩa là không có khả năng xảy ra) đến 1 (nghĩa là có khả năng chắc chắn rằng tài sản sinh lời ở một tỷ suất cụ thể) và thông thường được ước tính một cách chủ quan dựa trên số liệu quá khứ của tài sản hay của những tài sản tương tự nhau được điều chinh theo dự đoán của nhà đầu tư về triển vọng của tài sản trong tương lai. Chẳng hạn, nhà đầu tư dự đoán khoảng 30% khả năng rằng tỷ suất lợi tức của một tài sản đơn được chọn mang lại 10%. Sử dụng những thông tin dự đoán trong tương lai liên quan đến các triển vọng của nền kinh tế, nhà đầu tư có thể lượng hóa được những nhân tố tác động đến danh mục đầu tư của họ trong tương lai.
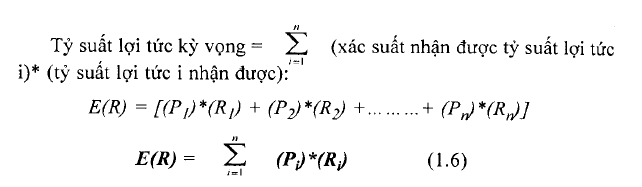
Trong đó: Pj là xác suất xảy ra trạng thái i và Rj là tỷ suất lợi tức của chứng khoán ở trạng thái i và n là số trạng thái.
Chúng ta hãy bắt đầu phân tích tác động của rủi ro thông qua một ví dụ về một cơ hội đầu tư với mức tỷ suất lợi tức chắc chắn là 5%. Hình 1.1 biểu diễn cho trường hợp này.
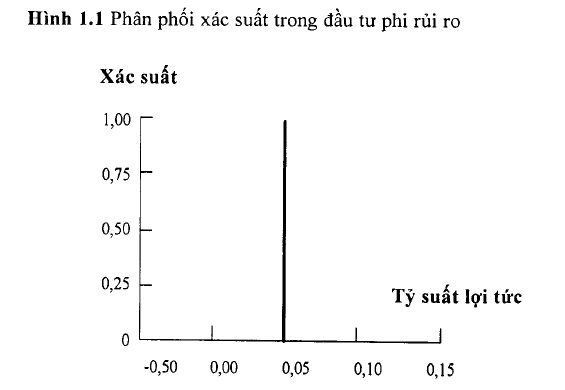
Bởi vì mức tỷ suất lợi tức thu được là chắc chắn, nên xác suất nhận được mức tỷ suất lợi tức này bằng 1. Thực tế có rất ít cơ hội đầu tư có thể đảm bảo thu được một mức tỷ suất lợi tức chắc chắn. Trong trường hợp này, chi có một giá trị P*Rị duy nhất:
E(Rị) = (1,0)*(0,05) = 0,05.
Trong một tình huống khác, giả sử nhà đầu tư tin rằng cơ hội đầu tư sẽ mang lại nhiều mức tỷ suất lợi tức khác nhau phụ thuộc vào trạng thái của nền kinh tế. Chẳng hạn, xem xét ví dụ dưới đây:
Một nhà đầu tư ước lượng xác suất của mỗi tỷ suất lợi tức tương ứng với từng trạng thái của nền kinh tế dựa trên trải nghiệm quá khứ và triển vọng hiện tại của nền kinh tế:

Tập hợp các kết quả có thể có, được biểu diễn trên Hình 1.2.
Tỷ suất lợi tức kỳ vọng [E(Rị)] được tính toán như sau:
E(Rị) = [(0,15)*(0,20)] + [(0,15)*(-0,20)] + [(0,70)*(0,10)] – 0,07 = 7%.
Hình 1.2 Phân phối xác suất của một cơ hội đầu tư có rủi ro với 3 mức tỷ suất lợi tức
Xác suất
0,80 ”
0,60 ~~
0,40 ~
- 20 “ I
—I_____ I____ L——– 1———-
0 -0,30 -0,20 -0,10 0,00 0,10
Xem xét một trường hợp khác với một chuỗi mười tỷ suất lợỉ tức từ -40% đến 50% với xác suất như nhau cho từng mức lợi tức. Đồ thị với tập hợp các lợi tức mong đợi được biểu diễn trên Hình 1.3.
E(R¡) = 0,10*(-0,40) + 0,10*(-0,30) + 0,10*(-0,20) + 0,10*(-0,10) + o, 10*0,0 + o, 10*0,1 o + o, 10*0,20 + o, 10*0,30 + o, 10*0,40 + o, 10*0,50
= (-0,04) + (-0,03) + (-0,02) + (-0,01) + 0,00 + 0,01 + 0,02 + 0,03 + 0,04 + 0,05
= 0,05.
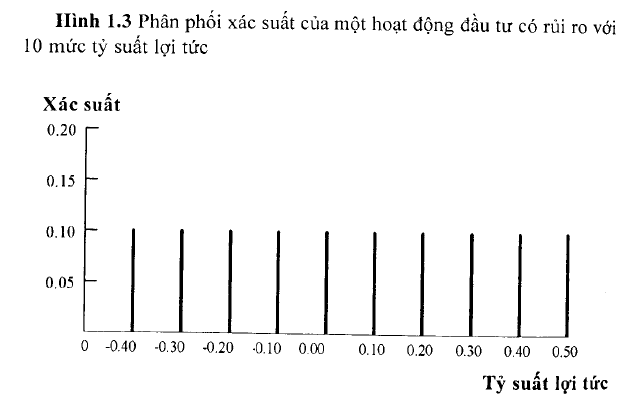
Tỷ suất lợi tức kỳ vọng đối với cơ hội đầu tư này bằng với tỷ suất lợi tức trong trường hợp cơ hội đầu tư có tỷ suất lợi tức chắc chắn 5%; nhưng trong trường hợp này, nhà đầu tư không chắc chắn về tỷ suất lợi tức thực tế thu được. Do sự không chắc chắn nên cơ hội này được xem như là một hoạt động đầu tư có rủi ro. Kết quả là nhà đầu tư sẽ phải cân nhắc để lựa chọn giữa một cơ hội đầu tư có rủi ro và một cơ hội đầu tư phi rủi ro thay thế.
Những nhân tố quyết định đén tỷ suất lọi tức kỳ vọng
Vấn đề mấu chốt của quá trình lựa chọn loại chứng khoán cho danh mục là tìm được loại chứng khoán với tỷ suất lợi tức bù đắp được: (i) giá trị thời gian của tiền tệ, (ii) tỳ lệ lạm phát dự đoán và (iii) mức độ rủi ro. Như vậy, ba yếu tố trên sẽ chi phổi tỷ suất lợi tức yêu cầu (kỳ vọng). Đây là mức tỷ suất lợi tức thấp nhất mà nhà đầu tư mong đợi từ việc đầu tư để chấp nhận trì hoãn tiêu dùng hiện tại. Do sự khác nhau về tỷ suất lợi tức nhận được của mỗi tài sản, nhà đầu tư phải năm vững những nhân tố rủi ro ảnh hưởng đến tỷ suất lợi tức kỳ vọng và sử dụng chúng để đánh giá các cơ hội đầu tư.

31 Th12 2020
31 Th12 2020
30 Th12 2020
31 Th12 2020
30 Th12 2020
31 Th12 2020