Kinh tế quốc tế
Thuyết cân bằng tổng quát
1. Thuyết cân bằng tổng quát đối với nền kinh tế tự cung tự cấp
1.1. Đường cung
Đầu tiên, xuất phát từ đường cong chuyển đổi và đường cung của hai loại hàng hóa, ta xây dựng được một hàm số về tỷ số giá hoặc giá tương đối, pB/ pA. Tham chiếu với hình 3.6a, giả sử rằng pB/pA bằng tan α, điểm tối ưu nằm trên đường cong chuyển đổi được xác định là điểm H, tại đây tỷ lệ chuyển đổi cận biên và giá tương đối có giá trị bằng nhau. Do đó, số lượng hàng hóa A là OA’ và số lượng hàng hóa B là OB’ sẽ được cung cấp ra thị trường với mức giá tương đối là tan α. Tương tự, khối lượng hàng hóa A là OAE và khối lượng hàng hóa B là OBE sẽ được cung cấp ra thị trường khi pB/pA là tan β. Một cách ngắn gọn hơn, tương ứng với mỗi tỷ số giá phù hợp sẽ chỉ có một sự kết hợp duy nhất về sản lượng sản xuất hàng hóa A và B.
Trong hình 3.6b, tỷ số giá được đo lường trên trục dọc và sản lượng của hai loại hàng hóa được đo lường trên trục ngang. Việc tăng sản lượng của hàng hóa A được đo từ điểm O về phía bên phải và sự gia tăng sản lượng của hàng hóa B được đo từ điểm O về phía bên trái. Giả sử mức giá tương đối OP = tan α, sản lượng hàng hóa A là OA’ và sản lượng hàng hóa B tương ứng là OB’, sự kết hợp này được biểu diễn bằng điểm H trong hình 3.6a. Như vậy, chúng ta có được hai điểm HA và HB trong hình 3.6b. Vì OA’ là sản lượng hàng hóa A được cung khi mức giá tương đối đạt OP nên điểm HA nằm trên đường cung của hàng hóa B.
Hình 3.7: Đường cong chuyển đổi, đường cung và xác định điểm cân bằng tổng quát trong nền kinh tế đóng
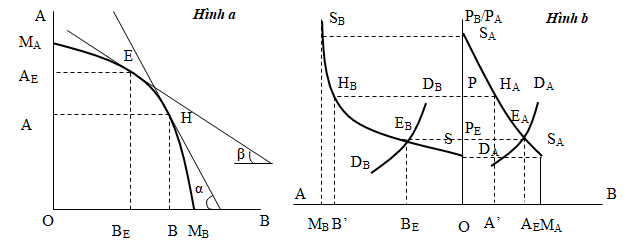
Nguồn: Gandolfo (2014)
Cũng theo cách này, chúng ta có được đường cung của hàng hóa A, SASA và đường cung của hàng hóa B, SBSB. Đây được gọi là đường cung cân bằng tổng thể. Cả hai đường cung đều hướng lên tương ứng với sự tăng lên của mức giá tương đối: SBSB tăng lên tương ứng với pB/pA (mức giá tương đối của hàng hóa B so với hàng hóa A) và SASA tăng lên tương ứng với pa/pb (mức giá tương đối của hàng hóa A so với hàng hóa B). Tuy nhiên, vì SASA cũng là đồ thị của hàm pB/pA nên nó sẽ đơn điệu giảm vì pb/pa giảm khi pA/pB tăng.
Giao điểm của đường cong SASA với trục tung tương ứng với tỷ số giá và trùng với điểm MB, đây là điểm tối ưu trên đường cong chuyển đổi (hình 3.7a). Tại đây, sản lượng hàng hóa A là 0 tương ứng với sản lượng của hàng hóa B đạt cực đại, nghĩa là tất cả các yếu tố sản xuất đều được huy động vào sản xuất hàng hóa B (để đơn giản giả định rằng độ dốc của đường cong chuyển đổi không phải vô hạn tại điểm MB và không bằng 0 tại MA. Điều này biểu hiện bằng phần thẳng đứng của đường cong SBSB tương ứng với MOB trong hình 3.7b để thấy rằng tại điểm này, không thể sản xuất thêm một đơn vị hàng hóa B nào nữa.
Tương tự như vậy, giao điểm của đường cong SBSB với trục tung tại một điểm mà tỷ số giá tạo nên điểm tối ưu trên đường cong chuyển đổi và trùng với điểm MA (hình 3.7a). Tại điểm này, sản lượng của hàng hóa B bằng 0 tương ứng với sản lượng của hàng hóa A đạt cực đại, như trên đồ thị được thể hiện bởi độ dài OMA.
1.2. Đường cầu
Bước thứ hai là vẽ đường cầu của hai loại hàng hóa theo phương trình pb = pa. Như đã được trình bày ở trên, với mỗi mức tỷ số giá tại một điểm nằm trên quỹ tích hiệu quả trong sơ đồ hộp tương ứng với một điểm trên đường cong chuyển đổi, từ đó xác định được năng suất vốn và lao động cận biên, mỗi mức năng suất chỉ phụ thuộc vào tỷ lệ các yếu tố khi các chức năng sản xuất đồng nhất. Trong trạng thái cân bằng cạnh tranh, nhuận thu được từ sử dụng các yếu tố sản xuất trùng với năng suất cận biên của chúng. Như vậy, từ sự phân bổ các yếu tố sản xuất có thể xác định được lợi nhuận thực tế thu về. Trên thực tế, một mức thu nhập thực tế của mỗi cá nhân tương ứng với mỗi tỷ số giá có nghĩa là thu nhập thực tế của mỗi cá nhân luôn thay đổi khi giá tương đối thay đổi. Với thu nhập của mình, tại mỗi mức giá tương đối các cá nhân thường cố gắng tìm cách tối đa hóa lợi ích, từ đó xác định được lượng cầu về hàng hóa A và B. Cộng tổng lượng cầu về hàng hóa A và B của các cá nhân sẽ thu được tổng cầu trong nền kinh tế đối với hai loại hàng hóa này. Nếu lặp lại bước này tại mỗi tỷ số giá có thể pb = pa, chúng ta thu được đường tổng cầu đối với hàng hóa A và B theo công thức pa = pb.
Cần nhấn mạnh rằng những đường cầu đối với hàng hóa A và B biểu diễn lượng cầu hàng hóa theo hàm số giá tương đối được xây dựng dựa trên giả định các yếu tố khác không đổi, điều này khác với đường cầu Marshallian hoặc đường cầu cân bằng cục bộ. Ngược lại, khi pb và pa không bằng nhau thì chúng ta nằm tại một điểm khác trên đường cong chuyển đổi và trên quỹ tích lợi ích. Do đó, năng suất cận biên của các yếu tố sẽ khác nhau. Nói cách khác, đường cầu chúng ta đang xây dựng phụ thuộc vào mức giá tương đối và thu nhập thực tế là đường cầu cân bằng tổng thể. Tuy nhiên, vì giả định rằng thu nhập thực tế chỉ phụ thuộc vào mức giá tương đối nên đường cầu chỉ là hàm của mức giá tương đối.
Để đơn giản, chúng tôi giả định rằng đường cầu giảm với sự tăng lên của mức giá tương đối, do vậy DADA giảm khi pb = pa tăng lên.
1.3. Trạng thái cân bằng tổng quát và định luật Walras
Bước cuối cùng là xây dựng đường cung và đường cầu trên cùng một đồ thị như hình 3.6b. Giao điểm giữa đường cung và đường cầu được gọi là điểm cân bằng cung cầu, lần lượt là EA và EB tương ứng với hàng hóa A và B. Sản lượng cân bằng tương ứng lần lượt là OAE và OBE, và tỷ số giá cân bằng tương đối là OPE, bằng tan β. Điểm cân bằng nằm trên đường cong chuyển đổi, như vậy việc phân bổ các yếu tố sản xuất giữa hai ngành, từ đó xác định được năng suất cận biên, lợi nhuận thực tế mà việc sử dụng các yếu tố sản xuất mang lại và sự phân bổ thu nhập. Như vậy, trạng thái cân bằng tổng thể của nền kinh tế được thành lập.
Trong hình 3.7b, chúng ta mặc định rằng mức giá tương đối trên hai thị trường bằng nhau. Sự cân bằng này được sử dụng làm cơ sở vì nếu tại hai thị trường cân bằng có mức giá tương đối khác nhau thì mô hình sẽ không phù hợp. Dựa trên định luật Walras, có thể kết luận rằng nếu một thị trường đang trong trạng thái cân bằng thì thị trường còn lại cũng cân bằng, do đó tỷ số giá cân bằng phải bằng nhau ở cả hai thị trường.
Gọi pk và pl là lợi nhuận thu được từ việc sử dụng các yếu tố sản xuất, SA và SB là lượng cung hàng hóa A và B, K và L là lượng các yếu tố sản xuất phân bổ vào lĩnh vực sản xuất hàng hóa A và B. Trong mỗi ngành sản xuất, tổng giá trị các yếu tố đầu vào đúng bằng tổng giá trị đầu ra. Điều này đúng với quy mô không đổi, đồng thời cũng đúng đối với bất kỳ hàm sản xuất nào nếu phí nhập khẩu bằng không và không có sự cạnh tranh từ các doanh nghiệp khác. Như vậy ta có được:
Pk ka + plla = Pasa
Pkkb + pllb = pbsb
Như vậy
pK (KA + KB) + pL(LA + LB) = pASA + pBSB (3.6)
Vế bên trái của phương trình 3.6 là tổng thu nhập của tất cả các cá nhân trong nền kinh tế (thu nhập từ hoạt động bán dịch vụ và các yếu tố sản xuất của mình). Vì toàn bộ thu nhập được dùng để mua hàng hóa A và B nên chúng ta có thể viết lại như sau:
pK(KA + KB) + pL(LA + LB) = pADA + pBDB (3.7)
Với DA và DB là lượng cầu đối với hai loại hàng hóa, phương trình 3.7 là phương trình tổng ngân sách ràng buộc. Phương trình 3.6 và 3.7 có hai vế phải bằng nhau và hai vế trái bằng nhau nên:
pADA + pBDB = pASA + pBSB (3.8)
Từ đó:
pA(DA – SA) + pB(DB – SB) = 0 (3.9)
Phương trình 3.9 đúng với bất kỳ giá trị hợp lý nào của pa và pb. Dạng phương trình 3.8 khẳng định rằng tổng giá trị của các hàng hóa được yêu cầu cần phải bằng với tổng khối lượng hàng hóa cung ứng ra thị trường; dạng phương trình 3.9 khẳng định rằng tổng khối lượng hàng hóa được yêu cầu dư thừa phải bằng 0. Mối quan hệ này được gọi là định luật Walras. Nhìn chung, n thị trường liên kết với sự ràng buộc ngân sách, định luật Walras ngụ ý rằng nếu n – 1 thị trường nằm trong trạng thái cân bằng thì thị trường thứ n cũng nằm trong trạng thái cân bằng. Trong trường hợp trên chỉ gồm hai thị trường, do đó nếu thị trường này nằm trong trạng thái cân bằng thì thị trường còn lại cũng cân bằng. Ví dụ, nếu DA = SA thì theo phương trình 3.9 thì DB = SB.
2. Thuyết cân bằng tổng quát đối với nền kinh tế mở
Mở rộng hơn đối với nền kinh tế mở, giả định trên thị trường chỉ gồm hai quốc gia (trong đó quốc gia 1 là nước chủ nhà và quốc gia 2 là phần còn lại của nền kinh tế thế giới) và không có chi phí vận chuyển, thị trường cạnh tranh hoàn hảo; cả hai quốc gia đều sử dụng các yếu tố sản xuất như nhau và không dịch chuyển giữa quốc gia này sang quốc gia khác, và cùng sản xuất các loại hàng hóa như nhau.
Do giả định rằng không tồn tại thương mại quốc tế, cả hai quốc gia đều nằm trong trạng thái cân bằng tương tự như mô tả trong hình 3.7b. Tuy nhiên, do sự khác nhau về nguồn vốn và phân bổ vốn, công nghệ và tình hình chung của hai quốc gia là khác nhau nên tỷ số giá cân bằng giữa hai quốc gia không giống nhau. Do vậy, không có cơ hội cho sự tồn tại của thương mại quốc tế. Giả sử trong hai nền kinh tế đóng này, tỷ số giá cân bằng của hai nước hoàn toàn khác nhau, và để đảm bảo tính tổng quát, giả sử tỷ số giá của quốc gia thứ 2 lớn hơn quốc gia thứ nhất như trong sơ đồ đối ứng 3.8. Trong hình 3.8, đường cung và đường cầu được vẽ cho hai loại hàng hóa như nhau ở cả hai nước, phần bên phải là đường cung và đường cầu của hàng hóa A của quốc gia 1 và phần bên trái là của hàng hóa A ở quốc gia 2. Như đã giả định ở trên, tỷ số giá cân bằng trong nền kinh tế đóng của quốc gia 2 (ORE) lớn hơn của quốc gia 1 (OPE).
Hình 3.8: Xác định trạng thái cân bằng quốc tế
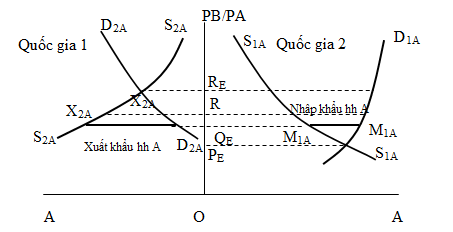
Nguồn: Gandolfo (2014)
Dễ dàng nhận thấy rằng khi mở cửa thương mại, quan hệ thương mại chỉ có thể diễn ra nếu có sự thống nhất giữa hai quốc gia về tỷ số giá cân bằng (tỷ số này gọi là tỷ số giá quốc tế). Trong trường hợp quan hệ thương mại tự do giữa hai nước, điều kiện cạnh tranh hoàn hảo và không có chi phí vận chuyển, với cùng một mặt hàng phải có mức giá bằng nhau ở cả thị trường hai nước, như vậy tỷ số giá quốc tế và tỷ số giá trong nước mới bằng nhau. Tương tự như vậy, khi tỷ số giá quốc tế cao hơn ORE, cả hai quốc gia đều có nhu cầu mua hàng hóa A của quốc tế và như vậy cầu hàng hóa A ở cả hai quốc gia đều dư và thị trường không thể đạt được trạng thái cân bằng. Trường hợp tỷ số giá quốc tế thấp hơn OPE, cả hai quốc gia sẽ tăng cường cung ứng hàng hóa A ra quốc tế và cung sẽ vượt cầu, thị trường quốc tế không cân bằng. Như vậy, chỉ khi các điều luật thương mại quốc tế được cân nhắc giữa OPE và OPE mà quốc gia 1 yêu cầu và quốc gia 2 cung ứng.
Trạng thái cân bằng quốc tế được thiết lập tại một điểm mà mức dư cầu của quốc gia đối với hàng hóa A chính xác bằng mức dư cung của quốc gia 2 đối với hàng hóa này. Trong hình 3.8, tại mức giao dịch quốc tế là OQE, M1AM1A = X2AX2A.
Nếu cả hai quốc gia đang trong trạng thái cân bằng tại điểm RE thì sẽ không có nhu cầu mua bất kỳ hàng hóa nào từ bên ngoài. Ngược lại, nếu quốc gia 1 có dư cầu về hàng hóa A (ORE), theo định luật Walras, phần cung hàng hóa B dư thừa sẽ được chuyển sang quốc gia 1, do đó quốc gia này có nhu cầu nhập khẩu hàng hóa B và xuất khẩu hàng hóa A. Nhưng vì quốc gia 2 không có nhu cầu về hàng hóa B hay cung ứng hàng hóa A nên thị trường thế giới sẽ dư cung hàng hóa B và dư cầu hàng hóa A nên giá tương đối quốc tế của hàng hóa B theo A giảm, ví dụ là OR.
Khi điều khoản thương mại là OR, tại quốc gia 1 mức dư cầu hàng hóa A (và mức dư cung hàng hóa B) giảm dẫn đến mức dư cung hàng hóa A (và mức dư cầu hàng hóa B) tại quốc gia 2. Dễ dàng nhận thấy rằng mức dư cầu hàng hóa A tại quốc gia 1 lớn hơn mức dư cung hàng hóa này tại quốc gia 2 dẫn đến mức dư cầu hàng hóa A (và dư cung hàng hóa B) trên thị trường thế giới. Quá trình này tiếp tục diễn ra cho đến khi đạt được điểm QE (mức dư cầu hàng hóa A tại quốc gia 1 chính xác bằng mức dư cung hàng hóa này tại quốc gia 2). Trên thị trường quốc tế đối với sản phẩm A, sự cân bằng cung cầu tại sản lượng giao dịch OQE (thị trường quốc tế đối với hàng hóa B cũng cân bằng). Quốc gia 1 sẽ nhập khẩu một lượng M1AM1A hàng hóa A, chính xác bằng lượng X2AX2A hàng hóa này quốc gia 2 xuất khẩu. Tương tự như vậy (nhưng ngược lại) đối với việc quốc gia 1 xuất khẩu và quốc gia 2 nhập khẩu hàng hóa B.
Kết luận, trong mô hình thương mại quốc tế tân cổ điển, sự tồn tại của mối quan hệ thương mại, loại hình và khối lượng giao dịch thương mại, điều kiện thương mại dưới tác động tổng hợp của sự phân bổ yếu tố sản xuất, công nghệ, thị hiếu tạo nên trạng thái cân bằng tổng quát. Đây là kết quả của định luật Walras đối với nền kinh tế mở.
Trong mỗi quốc gia, tổng giá trị nhu cầu bằng tổng giá trị cung ứng (phương trình 3.8) và đặt 1 và 2 tương ứng với quốc gia 1 và quốc gia 2, chúng ta có được:
pAD1A + pBD1B = pAS1A + pBS1B;
pAD2A + pBD2B = pAS2A + pBS2B (3.10)
và
pA(D1A + D2A) + Pb(D1B + D2B) = pA(S1A + S2A) + pB(S1B + S2B) (3.11)
Vì tổng nhu cầu quốc tế bằng tổng cung ứng quốc tế nên phương trình trên được viết thành
pA(D1A – S1A) + (D2A – S2A) + pB(D1B – S1B) + (D2B – S2B) = 0 (3.12)
nghĩa là tổng giá trị của mức dư cầu quốc tế phải bằng 0 tại bất kỳ mức giá hợp lý pa và pb nào.
Theo phương trình 3.10, không quốc gia nào chỉ nhập khẩu hoặc xuất khẩu hàng hóa. Như vậy
pA(D1A – S1A) = pB(S1B – D1B) ;
pA(D2A – S2A) = pB(S2B – D2B) (3.13)
nếu D1A> S1A thì S1B >D1B. Phương trình 3.13 là như nhau đối với mỗi quốc gia và giá trị xuất khẩu của các loại hàng hóa đều được đo lường bằng giá quốc tế tương đối. Như vậy, về mặt lý thuyết thương mại quốc tế thì cán cân thương mại luôn thăng bằng.
Nguồn: Nguyễn Hoàng Quy và cộng sự (2016), Marketing nhân sự, NXB Thống kê.

2 Th8 2022
3 Th8 2022
2 Th8 2022
29 Th7 2022
29 Th12 2021
2 Th8 2022