Đầu tư tài chính
Lựa chọn danh mục đầu tư tối ưu
1. Lựa chọn danh mục đầu tư tối ưu trong trường hợp không tồn tại tài sản phi rủi ro
Chúng ta thấy rằng đường biên hiệu quả bao gồm tập hợp các danh mục đầu tư hiệu quả mà nhà đầu tư có thể lựa chọn để tiến hành đầu tư. Việc chọn một danh mục đầu tư hiệu quả từ đường biên hiệu quả là tùy thuộc vào hệ số ngại rủi ro của nhà đầu tư. Chúng ta cũng biết rằng các nhà đầu tư luôn muốn tối đa hóa giá trị hữu dụng có thể có từ các cơ hội đầu tư sẵn có. Hay nói cách khác, các đường cong hữu dụng đồng nhất cao hơn luôn được lựa chọn hơn các đường cong hữu dụng đồng nhất thấp. Kết hợp hai điều kiên này lại với nhau: khỉ không tồn tại tài sản phi rủi ro, danh mục đầu tư tối ưu mà nhả đầu tư sẽ chọn ¡à danh mục nằm trên đường biên hiệu quả và tại đỏ đường biên hiệu quả tiếp xức với đường cong hữu dụng đồng nhất.
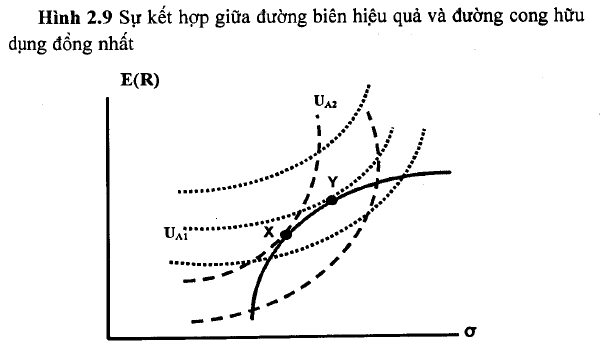
Trên Hình 2.9, X là danh mục đầu tư tối ưu mà nhà đầu tư có hệ số ngại rủi ro A2 sẽ chọn. Trong khi đó, Y là danh mục đầu tư tối ưu mà nhà đầu tư có hệ số ngại rủi ro A| sẽ chọn.
2. Lựa chọn danh mục đầu tư tối ưu trong trường hợp tồn tại tài sản phi rủi ro
Giả thiết tồn tại tài sản phi rủi ro đóng vai trò quan trọng trong lý thuyết định giá tài sản (sẽ được thảo luân trong chưomg 3). Trong phần này, chúng ta sẽ xem xét ảnh hưởng của tài sản phi rủi ro đến tỷ suất lợi tức kỳ vọng và rủi ro của danh mục đầu tư khi tài sản phi rủi ro được kết hợp với một danh mục đầu tư rủi ro trên đường biên hiệu quả Markowitz.
Tài sản phi rủi ro là tài sản mang lại một tỷ suất lợi tức kỳ vọng chắc chắn. Do vậy, độ lệch chuẩn của tỷ suất lợi tức trên tài sản phi rủi ro bằng không (ơ = 0). Tương tự, hiệp phương sai (hay hệ số tương quan) giữa tài sản phi rủi ro với bất kỳ tài sản rủi ro hay danh mục các tài sản đầu tư rủi ro cũng bằng không. Khi kết hợp một tài sản phi rủi ro với một danh mục các tài sản đầu tư rủi ro, tỷ suất lợi tức kỳ vọng của danh mục đầu tư mới này được xác định như công thức (2.1) đã chỉ rõ trước đây:

Chúng ta thấy rằng độ lệch chuẩn và tỷ suất lợi tức kỳ vọng của danh mục kết hợp giữa tài sản phi rủi ro và danh mục các tài sản rủi ro có quan hệ tuyến tính với nhau. Giả sử danh mục đầu tư rủi ro là một danh mục được chọn trên đường biên Markowitzrìrì (chẳng hạn danh mục A). Khi đó kết hợp giữa tài sản phi rủi ro và danh mục A theo một tỷ trọng y nào đó sẽ cho chúng ta một danh mục đầu tư kết hợp nằm trên đường thẳng đi qua Rf và A (Hình 2.10 dưới đây). Phương trình của đường thẳng đi qua Rf và A có dàng như phương trình (2.3). Với bất kỳ danh mục đầu tư nào nằm trên đường biên Markowitz và dưới điểm A, chúng ta luôn tim được một danh mục đầu tư nằm trên đường RfA có cùng độ lệch chuẩn nhưng cung cấp tỷ suất lợi tức kỳ vọng cao hơn. Nói cách khác, các danh mục đầu tư nằm trên đường RfA cung cấp cơ hội rủi ro – lợi tức tốt hơn các danh mục tương ứng nằm trên đường biên Markowitz và dưới đỉểm A. Tiếp tục, nếu chúng ta chọn danh mục đầu tư B trên đường biên Markowitz, chúng ta có thể tạo ra một danh mục nào đó nằm trên đường RfB bằng cách đầu tư tỷ trọng y (0 < y < 1) vào danh mục B và (1- y) vào tài sản phi rủi ro. Tương tự, các danh mục đầu tư nằm trên đường RfB cung cấp cơ hội rủi ro-lợi tức tốt hơn các danh mục tương ứng nằm trên đường biên Markowitz và dưới điểm B (kể cả các danh mục nằm trên đường RfA).
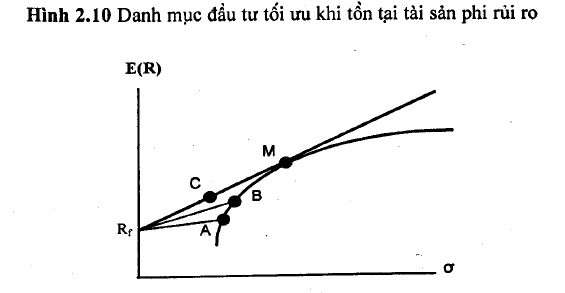
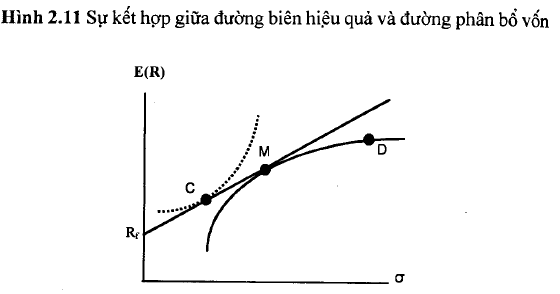
Chúng ta cỏ thể tiếp tục chọn các danh mục tài sản rủi ro nằm trên ng biên Markowitz và cao hon điểm B cho đến khi đạt đến điểm M lỏ đường thẳng xuất phát tại Rf tiếp xúc với đường biên Markowitz, mg ta thấy rằng các danh mục đầu tư nằm trên đường RfM cung cấp lội rủi ro – lợi tức tốt hon bất kỳ danh mục nào tương ứng nằm dưới n M. Đường RjM đại diện cho tập hợp các danh mục đầu tư hiệu quả nhà đầu tư có thể lựa chọn
Sau khi đã xác định được tập hợp các danh mục đầu tư hiệu quà, nhà đầu tư sẽ lựa chọn danh mục đầu tư tối ưu dựa vào hệ sổ ngại “O của họ. Danh mục đầu tư tối ưu cụ thể mà nhà đầu tư sẽ chọn là ti mục nằm trên đường thẳng RfM và tại đó đường RfM tiếp xúc với ng cong hữu dụng của nhà đầu tư đó (ví dụ: điểm c trên Hình 2.11 )•
* Đầu tư bằng cách sử dụng đòn bẫy tài chính (vay nợ)
Chúng ta có thể đặt câu hỏi rằng: Có thể đạt được tỷ suất lợi tức kỳ l cao hơn tỷ suất lợi tức kỳ vọng tại điểm M hay không nếu như nhà tư sẵn sàng chấp nhận rủi ro cao hơn? Câu trả lời là có.
Nhà đầu tư có hai lựa chọn như sau: (1) Đầu tư toàn bộ vào một danh mục nào đó trên đường biên Markowitz và nằm phía bên phải điểm M (chẳng hạn điểm D ở Hình 2.11); hoặc (2) Vay theo lãi suất phi rủi ro và đầu tư tất cả vào danh mục tài sản rủi ro M.
Giả sử nhà đầu tư vay theo lãi suất phi rủi ro với số tiền bằng 50% so với số vốn bỏ ra ban đầu. Bây giờ tỷ trọng đầu tư vào danh mục M sẽ là 150% (y = 1,5) và tỷ trọng đầu tư vào tài sản phi rủi ro sẽ là -50%.(13) Tỷ suất lợi tức kỳ vọng và độ lệch chuẩn của danh mục đầu tư kết hợp giữa danh mục M và sử dụng đòn bẩy là:
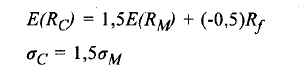
Trên đồ thị, danh mục này nằm trên đường thẳng đi qua Rf và M, về phía bên phải của điểm M. Một cách tổng quát, tất cả các danh mục nằm trên đường thẳng đi qua Rf và M, đồng thời nằm bên phải điểm M là các danh mục hiệu quả mà nhà đầu tư có thể lựa chọn trong ừường hợp có sử dụng đòn bẩy. Tương tự như các trường hợp trên, việc lựa chọn danh mục đầu tư tối ưu nhất định là tủy thuộc vào hệ sổ ngại rủi ro của nhà đầu tư.

31 Th12 2020
31 Th12 2020
31 Th12 2020
30 Th12 2020
31 Th12 2020
31 Th12 2020